L = загуба (ens, tbl, ResponseVarName)
L = загуба (ens, tbl, Y)
L = загуба (ens, X, Y)
L = загуба (___, име, стойност)
Описание
L = загуба (ens, tbl, ResponseVarName) връща грешката в класификацията за ансамбъл ens, изчислена с помощта на таблица на предиктори tbl и истински етикети на класове tbl.ResponseVarName .
L = загуба (ens, tbl, Y) връща класификационната грешка за ансамбъл ens, изчислена с помощта на таблица на предиктори tbl и истински етикети на класове Y .
L = загуба (ens, X, Y) връща грешката в класификацията за ансамбъл ens, изчислена с помощта на матрица от предиктори X и истински етикети на класове Y .
L = загуба (___, Име, Стойност) изчислява грешка в класификацията с допълнителни опции, посочени от един или повече аргументи Име, Стойност на двойка, като се използва някой от предишните синтаксиси.
Когато изчислява загубата, загубата нормализира вероятностите на класа в ResponseVarName или Y към вероятностите на класа, използвани за обучение, съхранени в свойството Prior на ens .
Аргументи за въвеждане
Класификационен ансамбъл, създаден с fitcensemble, или компактен класификационен ансамбъл, създаден с компактен .
Примерни данни, посочени като таблица. Всеки ред от tbl съответства на едно наблюдение, а всяка колона съответства на една променлива на предиктор. tbl трябва да съдържа всички предиктори, използвани за обучение на модела. Не са разрешени многоколонни променливи и клетъчни масиви, различни от клетъчни масиви със символни вектори.
Ако сте обучавали ens, използвайки примерни данни, съдържащи се в таблица, тогава входните данни за този метод също трябва да бъдат в таблица.
Име на променлива за отговор, посочено като име на променлива в tbl .
Трябва да посочите ResponseVarName като вектор на символи или скалар на низове. Например, ако променливата за отговор Y се съхранява като tbl.Y, тогава я посочете като 'Y'. В противен случай софтуерът третира всички колони от tbl, включително Y, като предсказатели при обучението на модела.
Матрица от данни за класификация. Всеки ред от X представлява едно наблюдение, а всяка колона представлява един предиктор. X трябва да има същия брой колони като данните, използвани за обучение на ens. X трябва да има същия брой редове като броя на елементите в Y .
Ако сте обучавали ens, използвайки примерни данни, съдържащи се в матрица, тогава входните данни за този метод също трябва да бъдат в матрица.
Етикети на наблюдения в клас в tbl или X. Y трябва да бъде от същия тип като класификацията, използвана за обучение на ens, и броят на елементите му трябва да е равен на броя редове от tbl или X .
Аргументи за двойка име-стойност
Посочете незадължителни двойки, разделени със запетая, на аргументи Name, Value. Name е името на аргумента, а Value е съответната стойност. Името трябва да се появи в кавичките. Можете да посочите няколко аргумента за двойка имена и стойност в произволен ред като Name1, Value1. NameN, ValueN .
Индекси на слаби учащи в ансамбъла, вариращи от 1 до ens .NumTrained. loss използва само тези обучаеми за изчисляване на загубата.
По подразбиране: 1: NumTrained
Функция за загуба, посочена като двойка, разделена със запетая, състояща се от „LossFun“ и вградено име на функция за загуба или манипулатор на функция.
Следващата таблица изброява наличните функции за загуби. Посочете такъв, като използвате съответния вектор от символи или скаларен низ.
| „бинодевианс“ | Биномиална девиантност |
| „класифициращ“ | Грешка в класификацията |
| „експоненциално“ | Експоненциално |
| "панта" | Панта |
| 'logit' | Логистика |
| „минимална цена“ | Минимални очаквани разходи за погрешно класифициране (за класификационни резултати, които са последващи вероятности) |
| "квадратичен" | Квадратичен |
„mincost“ е подходящ за класификационни резултати, които са вероятности отзад.
Ансамблите в пакети и подпространството връщат задните вероятности по подразбиране (ens.Method е 'Bag' или 'Subspace').
Ако методът на ансамбъла е „AdaBoostM1“, „AdaBoostM2“, GentleBoost или „LogitBoost“, тогава, за да използвате задните вероятности като класификационни резултати, трябва да посочите трансформацията на двойния лог, като въведете
За всички други ансамблови методи софтуерът не поддържа задните вероятности като класификационни резултати.
Посочете вашата собствена функция, като използвате нотация на функцията.
Да предположим, че n е броят на наблюденията в X и K е броят на отделните класове (numel (ens.ClassNames), ens е входният модел). Вашата функция трябва да има този подпис
Изходният аргумент lossvalue е скаларен.
Вие избирате името на функцията (lossfun).
C е n -by- K логическа матрица с редове, указващи към кой клас принадлежи съответното наблюдение. Редът на колоните съответства на реда на класа в ens.ClassNames .
Постройте C, като зададете C (p, q) = 1, ако наблюдението p е в клас q, за всеки ред. Задайте всички останали елементи на ред p на 0 .
S е n -by- K числова матрица на класификационни резултати. Редът на колоните съответства на реда на класа в ens.ClassNames. S е матрица от класификационни резултати, подобна на резултата от прогнозата .
W е n-by-1 числов вектор на теглата за наблюдение. Ако преминете W, софтуерът ги нормализира до сума 1 .
Разходите са цифрова матрица K-by-K на разходите за погрешна класификация. Например, Cost = one (K) - eye (K) определя цена от 0 за правилна класификация и 1 за погрешна класификация.
Посочете функцията си с помощта на 'LossFun', @ lossfun .
За повече подробности относно функциите на загуби вижте Класификация Загуба.
По подразбиране: „класифициращ“
Значение на изхода L:
'ансамбъл' - L е скаларна стойност, загуба за целия ансамбъл.
„индивид“ - L е вектор с един елемент на обучен обучаем.
„кумулативно“ - L е вектор, в който елемент J се получава чрез използване на учащи 1: J от входния списък на учащите.
По подразбиране: "ансамбъл"
Логическа матрица с размер N -by-T, където:
N е броят на редовете на X .
T е броят на слабите учащи се в ens .
Когато UseObsForLearner (i, j) е вярно, учащият j се използва при прогнозиране на класа на ред i на X .
По подразбиране: вярно (N, T)
Вектор на тежести за наблюдение, с неотрицателни записи. Дължината на тежестите трябва да е равна на броя редове в X. Когато посочите тегла, загубата нормализира тежестите, така че тежестите за наблюдение във всеки клас да се сумират до предварителната вероятност за този клас.
По подразбиране: единици (размер (X, 1), 1)
Изходни аргументи
Загуба на класификация, по подразбиране частта от погрешно класифицирани данни. L може да бъде вектор и може да означава различни неща, в зависимост от настройките на двойката име-стойност.
Примери
Грешка в оценката на класификацията
Заредете набора от данни за ириса на Fisher.
Обучете класификационен ансамбъл от 100 дървета за вземане на решения с помощта на AdaBoostM2. Посочете пънчета като слаби обучаеми.
Оценете класификационната грешка на модела, използвайки наблюденията на обучението.
Като алтернатива, ако ens не е компактен, тогава можете да оцените грешката в класификацията на учебната проба, като предадете ens на resubLoss .
Повече за
Загуба на класификация
Функциите на класификационните загуби измерват предсказващата неточност на класификационните модели. Когато сравнявате един и същ тип загуба сред много модели, по-ниската загуба показва по-добър предсказуем модел.
Обмислете следния сценарий.
L е среднопретеглената загуба на класификация.
n е размерът на извадката.
За двоична класификация:
yj е наблюдаваният етикет на класа. Софтуерът го кодира като –1 или 1, указвайки съответно отрицателния или положителния клас.
f (Xj) е суровият класификационен резултат за наблюдение (ред) j на данните за предсказване X.
mj = yj f (Xj) е класификационната оценка за класифициране на наблюдението j в класа, съответстващ на yj. Положителните стойности на mj показват правилната класификация и не допринасят много за средната загуба. Отрицателните стойности на mj показват неправилна класификация и допринасят значително за средната загуба.
За алгоритми, които поддържат многокласова класификация (т.е. K ≥ 3):
yj * е вектор на K - 1 нули, като 1 е в позицията, съответстваща на истинския, наблюдаван клас yj. Например, ако истинският клас на второто наблюдение е третият клас и K = 4, тогава y2 * = [0 0 1 0] ′. Редът на класовете съответства на реда в свойството ClassNames на входния модел.
f (Xj) е дължината K вектор на резултатите от класа за наблюдение j на данните предиктор X. Редът на резултатите съответства на реда на класовете в свойството ClassNames на входния модел.
mj = yj * ′ f (Xj). Следователно, mj е скаларната класификационна оценка, която моделът прогнозира за истинския, наблюдаван клас.
Тежестта за наблюдение j е wj. Софтуерът нормализира тежестите за наблюдение, така че те да се сумират към съответната вероятност от предходния клас. Софтуерът също нормализира предишните вероятности, така че те да се сумират на 1. Следователно,
Като се има предвид този сценарий, следната таблица описва поддържаните функции за загуба, които можете да зададете с помощта на аргумента двойка име-стойност 'LossFun'.
L = ∑ j = 1 n w j I < y ^ j ≠ y j >.
Класификационната грешка е претеглената част от погрешно класифицирани наблюдения, където y ^ j е етикетът на класа, съответстващ на класа с максимална задна вероятност. Аз< x> е индикаторната функция.
Софтуерът изчислява претеглените минимални разходи, използвайки тази процедура за наблюдения j = 1. n.
Оценете 1-K-вектор на очакваните разходи за класификация за наблюдение j:
γ j = f (X j) ′ C .
f (Xj) е векторът на колоната на вероятностите отзад на класа за двоична и многокласова класификация. C е матрицата на разходите, съхранявана от входния модел в свойството Cost.
За наблюдение j предскажете етикета на класа, съответстващ на минималните очаквани разходи за класификация:
y ^ j = min j = 1,., K (γ j) .
Използвайки C, идентифицирайте направените разходи (cj) за извършване на прогнозата.
Претеглената, средна, минимална загуба на разходи е
L = ∑ j = 1 n w j c j .
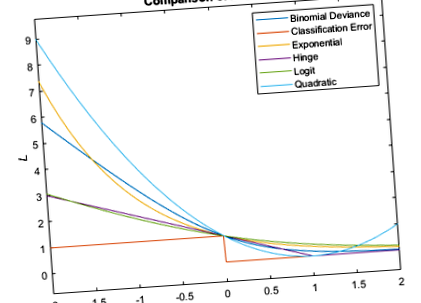
Тази цифра сравнява функциите на загубите (с изключение на „mincost“) за едно наблюдение над m. Някои функции са нормализирани да преминават през [0,1].
Разширени възможности
Високи масиви
Изчислете с масиви, които имат повече редове, отколкото се побират в паметта.
Тази функция напълно поддържа високи масиви. С тази функция можете да използвате модели, обучени на данни в паметта или на високи данни.
- Определете персонализиран претеглен класификационен слой - MATLAB; Simulink
- Загуба на класификация за линейни класификационни модели - MATLAB
- Загуба на класификация за модел на класификация на ядрото на Гаус - загуба на MATLAB
- Оценете точността на научените тегла на характеристиките на тестовите данни - MATLAB
- Оценете точността на научените тегла на характеристиките на тестовите данни - MATLAB