Оценете точността на научените тегла на характеристиките на тестовите данни
Синтаксис
грешка = загуба (mdl, X, Y)
грешка = загуба (mdl, X, Y, име, стойност)
Описание
err = загуба (mdl, X, Y) изчислява грешката в грешната класификация на модела mdl за предсказателите в X и етикетите на класовете в Y .
err = загуба (mdl, X, Y, Name, Value) изчислява класификационната грешка с допълнителни опции, посочени от един или повече аргументи за двойка име, стойност.
Аргументи за въвеждане
mdl - Модел за анализ на съседни компоненти за класификация
FeatureSelectionNCAClassification обект
Модел за анализ на компонент на квартал за класификация, върнат като FeatureSelectionNCAClassification обект.
X - Променливи стойности на предиктор
n-by-p матрица
Прогнозни стойности на променливи, посочени като n-by-p матрица, където n е броят на наблюденията и p е броят на предикторските променливи.
Типове данни: единичен | двойно
Y - Етикети на класове
категоричен вектор | логически вектор | числов вектор | низ масив | клетъчен масив от символни вектори с дължина n | символна матрица с n реда
Етикети на класове, посочени като категоричен вектор, логически вектор, числов вектор, масив от низове, масив от клетки с векторни символи с дължина n или матрица на символи с n редове, където n е броят на наблюденията. Елемент i или ред i от Y е етикетът на класа, съответстващ на ред i от X (наблюдение i).
Типове данни: единичен | двойно | логично | char | низ | клетка | категоричен
Аргументи за двойка име-стойност
Посочете незадължителни двойки, разделени със запетая, на аргументи Name, Value. Name е името на аргумента, а Value е съответната стойност. Името трябва да се появи в кавичките. Можете да посочите няколко аргумента за двойка имена и стойност в произволен ред като Name1, Value1. NameN, ValueN .
'LossFunction' - Тип функция за загуба
'Classiferror' (по подразбиране) | "квадратичен"
Тип функция за загуба, посочена като двойка, разделена със запетая, състояща се от „Функция за загуба“ и едно от следните.
„Classiferror“ - Грешка при погрешно класифициране, дефинирана като
1 n ∑ i = 1 n I (k i ≠ t i),
където k i е предсказаният клас, а t i е истинският клас за наблюдение i. I (k i ≠ t i) е индикаторът, когато k i не е същият като t i .
"квадратичен" - квадратична функция на загуба, дефинирана като
1 n ∑ i = 1 n ∑ k = 1 c (p i k - I (i, k)) 2,
където c е броят на класовете, p i k е вероятността за оценка, че i-то наблюдение принадлежи към клас k, а I (i, k) е индикаторът, че i-тото наблюдение принадлежи към клас k.
Пример: „LossFunction“, „квадратично“
Изходни аргументи
грешка - по-малка и по-добра мярка за точност на усвоените тегла на характеристиките
скаларна стойност
По-малка и по-добра мярка за точност на усвоени тегла на характеристиките, върната като скаларна стойност. Можете да посочите мярката за точност, като използвате аргумента LossFunction двойка име-стойност.
Примери
Настройте NCA модел за класификация
Заредете примерните данни.
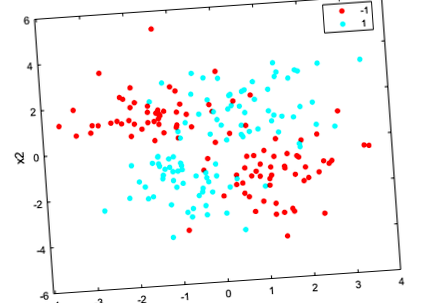
Създайте разпръснат график на данните, групирани по класа.
Добавете 100 неподходящи функции към. Първо генерирайте данни от нормално разпределение със средна стойност 0 и дисперсия 20.
Нормализирайте данните, така че всички точки да са между 0 и 1.
Поставете модела за анализ на компонент на квартал (NCA) към данните, като използвате стойността на Lambda по подразбиране (параметър за регулиране,). Използвайте LBFGS Solver и покажете информацията за конвергенцията.
Начертайте тежестите на характеристиките. Теглото на неподходящите характеристики трябва да бъде много близо до нула.
Предскажете класовете, използвайки NCA модел и изчислете матрицата на объркването.
Матрицата за объркване показва, че 40 от данните, които са в клас –1, се предвиждат като принадлежащи към клас –1. 60 от данните от клас –1 се предвиждат да бъдат в клас 1. По същия начин 94 от данните от клас 1 се предвиждат да са от клас 1 и 6 от тях се предвижда да са от клас –1. Точността на прогнозата за клас –1 не е добра.
Всички тежести са много близки до нулата, което показва, че стойността на използвания в обучението модел е твърде голяма. Когато всички тегла на характеристиките се доближават до нула. Следователно е важно да настроите параметъра на регуларизация в повечето случаи, за да откриете съответните характеристики.
Използвайте петкратна кръстосана проверка, за да настроите за избор на функция, като използвате fscnca. Настройката означава да се намери стойността, която ще доведе до минималната загуба на класификация. За да настроите с помощта на кръстосана проверка:
1. Разделете данните на пет гънки. За всяко сгъване cvpartition присвоява четири пети от данните като набор за обучение и една пета от данните като набор от тестове. Отново за всяка гънка, cvpartition създава стратифициран дял, където всеки дял има приблизително еднакъв дял от класове.
2. Обучете модела за анализ на компонента на квартала (nca) за всяка стойност, като използвате обучителния набор във всяка гънка.
3. Изчислете загубата на класификация за съответния набор от тестове в гънката, използвайки модела nca. Запишете стойността на загубата.
4. Повторете този процес за всички гънки и всички стойности.
Начертайте средните стойности на загубите на гънките спрямо стойностите. Ако стойността, която съответства на минималната загуба, попадне на границата на тестваните стойности, обхватът на стойностите трябва да бъде преразгледан.
Намерете стойността, която съответства на минималната средна загуба.
Поставете модела NCA на всички данни, като използвате най-добрата стойност. Използвайте LBFGS Solver и покажете информацията за конвергенцията.
Начертайте тежестите на характеристиките.
fscnca правилно установява, че първите две характеристики са подходящи, а останалите не. Първите две характеристики не са индивидуално информативни, но когато се вземат заедно, се получава точен модел на класификация.
Предскажете класовете, използвайки новия модел, и изчислете точността.
Матрицата на объркването показва, че точността на прогнозиране за клас –1 се е подобрила. 88 от данните от клас –1 се предвиждат да са от –1, а 12 от тях се предвиждат да са от клас 1. 92 от данните от клас 1 се предвиждат да са от клас 1 и 8 от тях се предвижда да бъдат от клас –1.
[1] Ян, В., К. Уанг, В. Цуо. „Избор на функция за компонент на квартала за данни с големи размери.“ Списание за компютри. Кн. 7, номер 1, януари 2012 г.
- Оценете точността на научените тегла на характеристиките на тестовите данни - MATLAB
- Загуба на класификация за модел на класификация на ядрото на Гаус - загуба на MATLAB
- Загуба на класификация за линейни класификационни модели - MATLAB
- Тест за чревни бактерии за отслабване Viome
- Мога ли да отслабна и тонус само с упражнения за плуване (мускули, вдигане на тежести) - Упражнение и