Загуба на класификация за линейни класификационни модели
Синтаксис
Описание
L = загуба (Mdl, X, Y) връща класификационните загуби за бинарния, линеен модел на класификация Mdl, използвайки предикторни данни в X и съответстващи етикети на класове в Y. L съдържа степен на грешка в класификацията за всяка степен на регуларизация в Mdl .
L = загуба (Mdl, Tbl, ResponseVarName) връща класификационните загуби за данните на предиктора в Tbl и истинските етикети на класове в Tbl.ResponseVarName .
L = загуба (Mdl, Tbl, Y) връща класификационните загуби за данните на предиктора в таблица Tbl и истинските етикети на класове в Y .
L = загуба (___, Име, Стойност) указва опции, използващи един или повече аргументи двойка име-стойност в допълнение към която и да е комбинация от входни аргументи в предишни синтаксиси. Например можете да посочите, че колоните в данните за предсказване съответстват на наблюдения или да посочите функцията за загуба на класификация.
Аргументи за въвеждане
Mdl - двоичен, линеен модел на класификация
ClassificationLinear модел обект
Двоичен, линеен модел на класификация, посочен като обект на ClassificationLinear модел. Можете да създадете обект ClassificationLinear модел, използвайки fitclinear .
X - Данни за предиктор
пълна матрица | оскъдна матрица
Данни предиктор, посочени като n-by-p пълна или оскъдна матрица. Тази ориентация на X показва, че редовете съответстват на отделни наблюдения, а колоните съответстват на отделни променливи предиктор.
Забележка
Ако ориентирате вашата предсказваща матрица така, че наблюденията да съответстват на колони и да посочите „ObservationsIn“, „колони“, тогава може да изпитате значително намаляване на времето за изчисление.
Дължината на Y и броят на наблюденията в X трябва да бъдат равни.
Типове данни: единичен | двойно
Y - Етикети на класове
категоричен масив | символен масив | низ масив | логически вектор | числов вектор | клетъчен масив от символни вектори
Етикети на класове, посочени като категоричен, символен или низ от масиви, логически или цифров вектор или масив от клетки на векторни знаци.
Типът данни на Y трябва да бъде същият като типа данни на Mdl.ClassNames. (Софтуерът третира масиви от низове като клетъчни масиви от символни вектори.)
Различните класове в Y трябва да са подмножество на Mdl.ClassNames .
Ако Y е масив от знаци, тогава всеки елемент трябва да съответства на един ред от масива.
Дължината на Y трябва да бъде равна на броя на наблюденията в X или Tbl .
Типове данни: категоричен | char | низ | логично | единичен | двойно | клетка
Tbl - Примерни данни
маса
Примерни данни, използвани за обучение на модела, посочени като таблица. Всеки ред на Tbl съответства на едно наблюдение, а всяка колона съответства на една променлива на предиктор. По желание Tbl може да съдържа допълнителни колони за променливата на реакцията и тежестите за наблюдение. Tbl трябва да съдържа всички предиктори, използвани за обучение на Mdl. Не са разрешени многоколонни променливи и клетъчни масиви, различни от клетъчни масиви със символни вектори.
Ако Tbl съдържа променливата за отговор, използвана за обучение на Mdl, тогава не е необходимо да указвате ResponseVarName или Y .
Ако тренирате Mdl, като използвате примерни данни, съдържащи се в таблица, тогава входните данни за загуба също трябва да са в таблица.
ResponseVarName - Име на променлива за отговор
име на променлива в Tbl
Име на променлива за отговор, посочено като име на променлива в Tbl. Ако Tbl съдържа променливата на отговора, използвана за обучение на Mdl, тогава не е необходимо да указвате ResponseVarName .
Ако посочите ResponseVarName, тогава трябва да го посочите като вектор на символи или скалар на низове. Например, ако променливата на отговора се съхранява като Tbl.Y, тогава посочете ResponseVarName като 'Y'. В противен случай софтуерът третира всички колони на Tbl, включително Tbl.Y, като предсказатели.
Променливата за отговор трябва да бъде категоричен, символен или низ от масив, логически или числов вектор или клетъчен масив от символни вектори. Ако променливата на отговора е символен масив, тогава всеки елемент трябва да съответства на един ред от масива.
Типове данни: char | низ
Аргументи за двойка име-стойност
Посочете незадължителни двойки, разделени със запетая, на аргументи Name, Value. Name е името на аргумента, а Value е съответната стойност. Името трябва да се появи в кавичките. Можете да посочите няколко аргумента за двойка имена и стойност в произволен ред като Name1, Value1. NameN, ValueN .
„LossFun“ - функция за загуба
'Classiferror' (по подразбиране) | „бинодевианс“ | „експоненциално“ | „панта“ | 'logit' | „минимална цена“ | "квадратичен" | дръжка на функцията
Функция за загуба, посочена като двойка, разделена със запетая, състояща се от „LossFun“ и вградено име на функция за загуба или манипулатор на функция.
Следващата таблица изброява наличните функции за загуби. Посочете такъв, като използвате съответния вектор от символи или скаларен низ.
| „бинодевианс“ | Биномиална девиантност |
| „класифициращ“ | Грешка в класификацията |
| „експоненциално“ | Експоненциално |
| "панта" | Панта |
| 'logit' | Логистика |
| „минимална цена“ | Минимални очаквани разходи за погрешно класифициране (за класификационни резултати, които са последващи вероятности) |
| "квадратичен" | Квадратичен |
„mincost“ е подходящ за класификационни резултати, които са вероятности отзад. За моделите на линейна класификация учениците с логистична регресия връщат задните вероятности като класификационни резултати по подразбиране, но учащите в SVM не го правят (вж. Прогнозиране).
Посочете вашата собствена функция, като използвате нотация на функцията.
Нека n е броят на наблюденията в X, а K е броят на отделните класове (numel (Mdl.ClassNames), където Mdl е входният модел). Вашата функция трябва да има този подпис:
Изходният аргумент lossvalue е скаларен.
Вие избирате името на функцията (lossfun).
C е n -by- K логическа матрица с редове, указващи класа, към който принадлежи съответното наблюдение. Редът на колоните съответства на реда на класа в Mdl.ClassNames .
Постройте C, като зададете C (p, q) = 1, ако наблюдението p е в клас q, за всеки ред. Задайте всички останали елементи на ред p на 0 .
S е n -by- K числова матрица на класификационни резултати. Редът на колоните съответства на реда на класа в Mdl.ClassNames. S е матрица от класификационни резултати, подобна на резултата от прогнозата .
W е n-by-1 числов вектор на теглата за наблюдение. Ако преминете W, софтуерът нормализира тежестите, за да сумира до 1 .
Разходите са K-by- K числова матрица на разходите за погрешна класификация. Например, Cost = one (K) - eye (K) определя цена от 0 за правилна класификация и 1 за погрешна класификация.
Пример: 'LossFun', @ lossfun
Типове данни: char | низ | функция_ръчка
„ObservationsIn“ - измерение за наблюдение на данни с предиктор
"редове" (по подразбиране) | "колони"
Измерение за наблюдение на данни с предиктор, посочено като двойка, разделена със запетая, състояща се от „ObservationsIn“ и „колони“ или „редове“ .
Забележка
Ако ориентирате вашата предсказваща матрица така, че наблюденията да съответстват на колони и да посочите „ObservationsIn“, „колони“, тогава може да изпитате значително намаляване на времето за изпълнение на оптимизацията. Не можете да посочите „ObservationsIn“, „колони“ за предсказващи данни в таблица.
„Тежести“ - тежести за наблюдение
единици (размер (X, 1), 1) (по подразбиране) | числов вектор | име на променлива в Tbl
Тегла за наблюдение, посочени като двойка, разделена със запетая, състояща се от „Тегла“ и числов вектор или името на променлива в Tbl .
Ако посочите Тегла като числов вектор, тогава размерът на Тегла трябва да бъде равен на броя на наблюденията в X или Tbl .
Ако посочите Weights като име на променлива в Tbl, тогава името трябва да бъде вектор на символи или скалар на низове. Например, ако тежестите се съхраняват като Tbl.W, тогава посочете Теглата като 'W'. В противен случай софтуерът третира всички колони на Tbl, включително Tbl.W, като предсказатели.
Ако предоставите тегла, тогава за всяка регулаторна сила, загубата изчислява претеглената класификационна загуба и нормализира теглата, за да сумира до стойността на предишната вероятност в съответния клас.
Типове данни: двойно | неженен
Изходни аргументи
L - Класификационни загуби
числов скалар | числов редовен вектор
Класификационни загуби, върнати като числов скаларен или редовен вектор. Тълкуването на L зависи от теглото и LossFun .
L е със същия размер като Mdl.Lambda. L (j) е класификационната загуба на линейния класификационен модел, обучен с помощта на регуларизационната сила Mdl.Lambda (j) .
Примери
Оценете загубата от класификация на тест-проба
Заредете NLP набора от данни.
X е оскъдна матрица от предсказващи данни, а Y е категоричен вектор на етикетите на класове. В данните има повече от два класа.
Моделите трябва да идентифицират дали броят на думите в дадена уеб страница е от документацията „Статистика и машинно обучение“ ™. И така, идентифицирайте етикетите, които съответстват на уеб страниците с документация на „Статистика и машинно обучение“ ™.
Обучете двоичен, линеен модел на класификация, който може да идентифицира дали броят на думите в уеб страницата на документацията е от документацията „Статистика и машинно обучение ™“. Посочете, за да проведете 30% от наблюденията. Оптимизирайте обективната функция, като използвате SpaRSA.
CVMdl е ClassificationPartitionedLinear модел. Той съдържа свойството Trained, което представлява масив от клетки 1 по 1, съдържащ модел ClassificationLinear, който софтуерът е обучил с помощта на обучителния набор.
Извлечете данните за обучение и тест от дефиницията на дяла.
Оценете грешката в класификацията на обучението и пробата.
Тъй като в CMdl има една сила на регуларизация, ceTrain и ceTest са числови скалари.
Задайте персонализирана загуба на класификация
Заредете NLP набора от данни. Предварително обработете данните, както е в Изчисление на загубата от класификация на тестови проби, и транспонирайте данните за предсказване.
Обучете двоичен, линеен модел на класификация. Посочете, за да проведете 30% от наблюденията. Оптимизирайте обективната функция, като използвате SpaRSA Посочете, че предикторните наблюдения съответстват на колони.
CVMdl е ClassificationPartitionedLinear модел. Той съдържа свойството Обучен, което е масив от клетки 1 по 1, съдържащ модел ClassificationLinear, който софтуерът е обучил с помощта на обучителния набор.
Извлечете данните за обучение и тест от дефиницията на дяла.
Създайте анонимна функция, която измерва линейна загуба, т.е.,
L = ∑ j - w j y j f j ∑ j w j .
w j е тежестта за наблюдение j, y j е отговор j (-1 за отрицателния клас и 1 в противен случай) и f j е суровият класификационен резултат от наблюдението j. Функциите за персонализирани загуби трябва да бъдат написани в определена форма. За правила за писане на персонализирана функция за загуба вижте аргумента двойка име-стойност LossFun.
Оценете загубата на класификация на обучението и тестовата проба, като използвате функцията за линейна загуба.
Намерете добро наказание за Ласо, като използвате загуба от класификация
За да определите добра сила на ласо-наказание за модел на линейна класификация, който използва обучаващ се в логистична регресия, сравнете процента на грешки в класификацията на тестовата проба.
Заредете NLP набора от данни. Предварително обработете данните, както е в Задайте персонализирана загуба на класификация.
Създайте набор от 11 логаритмично разположени регуларизационни степени от 1 0 - 6 до 1 0 - 0. 5 .
Тренирайте двоични модели с линейна класификация, които използват всяка от силите на регуларизацията. Оптимизирайте обективната функция, като използвате SpaRSA Намалете толеранса на градиента на целевата функция до 1e-8 .
Извлечете обучения модел на линейна класификация.
Mdl е обект на модел ClassificationLinear. Тъй като Ламбда е последователност на силите на регуларизация, можете да мислите за Mdl като 11 модела, по един за всяка сила на регуларизация в Ламбда .
Оценете грешката в класификацията на тестовата проба.
Тъй като има 11 силни страни на регуларизация, ce е 1 на 11 вектор на процента на грешки в класификацията.
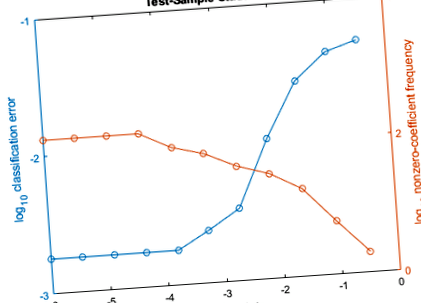
По-високите стойности на ламбда водят до прогностична променлива пропускливост, което е добро качество на класификатора. За всяка сила на регуларизация обучете линеен модел на класификация, използвайки целия набор от данни и същите опции, както когато сте кръстосали валидирането на моделите. Определете броя на ненулевите коефициенти на модел.
На същата фигура начертайте процентите на грешките на тестовата проба и честотата на ненулевите коефициенти за всяка сила на регулиране. Начертайте всички променливи в дневника.
Изберете индекса на силата на регуларизация, който балансира предикторска променлива рядкост и ниска класификационна грешка. В този случай трябва да е достатъчна стойност между 1 0 - 4 до 1 0 - 1.
Изберете модела от Mdl с избраната сила на регулиране.
MdlFinal е ClassificationLinear модел, съдържащ една регулаторна сила. За да изчислите етикети за нови наблюдения, предайте MdlFinal и новите данни за прогнозиране .
Повече за
Загуба на класификация
Функциите на класификационните загуби измерват предсказващата неточност на класификационните модели. Когато сравнявате един и същ тип загуба сред много модели, по-ниската загуба показва по-добър предсказуем модел.
Обмислете следния сценарий.
L е среднопретеглената загуба на класификация.
n е размерът на извадката.
За двоична класификация:
yj е наблюдаваният етикет на класа. Софтуерът го кодира като –1 или 1, указвайки съответно отрицателния или положителния клас.
f (Xj) е суровият класификационен резултат за наблюдение (ред) j на данните за предсказване X.
mj = yj f (Xj) е класификационната оценка за класифициране на наблюдението j в класа, съответстващ на yj. Положителните стойности на mj показват правилната класификация и не допринасят много за средната загуба. Отрицателните стойности на mj показват неправилна класификация и допринасят значително за средната загуба.
За алгоритми, които поддържат многокласова класификация (т.е. K ≥ 3):
yj * е вектор на K - 1 нули, като 1 е в позицията, съответстваща на истинския, наблюдаван клас yj. Например, ако истинският клас на второто наблюдение е третият клас и K = 4, тогава y2 * = [0 0 1 0] ′. Редът на класовете съответства на реда в свойството ClassNames на входния модел.
f (Xj) е дължината K вектор на резултатите от класа за наблюдение j на данните предиктор X. Редът на резултатите съответства на реда на класовете в свойството ClassNames на входния модел.
mj = yj * ′ f (Xj). Следователно, mj е скаларната класификационна оценка, която моделът прогнозира за истинския, наблюдаван клас.
Тежестта за наблюдение j е wj. Софтуерът нормализира тежестите за наблюдение, така че те да се сумират към съответната вероятност от предходния клас. Софтуерът също нормализира предишните вероятности, така че те да се сумират на 1. Следователно,
Като се има предвид този сценарий, следната таблица описва поддържаните функции за загуба, които можете да зададете с помощта на аргумента двойка име-стойност 'LossFun'.
L = ∑ j = 1 n w j I < y ^ j ≠ y j >.
Класификационната грешка е претеглената част от погрешно класифицирани наблюдения, където y ^ j е етикетът на класа, съответстващ на класа с максимална задна вероятност. Аз< x> е индикаторната функция.
Софтуерът изчислява претеглените минимални разходи, използвайки тази процедура за наблюдения j = 1. n.
Оценете 1-K-вектор на очакваните разходи за класификация за наблюдение j:
γ j = f (X j) ′ C .
f (Xj) е векторът на колоната на вероятностите отзад на класа за двоична и многокласова класификация. C е матрицата на разходите, съхранявана от входния модел в свойството Cost.
За наблюдение j предскажете етикета на класа, съответстващ на минималните очаквани разходи за класификация:
y ^ j = min j = 1,., K (γ j) .
Използвайки C, идентифицирайте направените разходи (cj) за извършване на прогнозата.
Претеглената, средна, минимална загуба на разходи е
L = ∑ j = 1 n w j c j .
Тази цифра сравнява функциите на загубите (с изключение на „mincost“) за едно наблюдение над m. Някои функции са нормализирани да преминават през [0,1].
Алгоритми
По подразбиране теглото за наблюдение е вероятност от предишен клас. Ако доставяте тежести с помощта на Тегла, тогава софтуерът ги нормализира, за да сумира до предишните вероятности в съответните класове. Софтуерът използва пренормализираните тегла, за да оцени претеглената класификационна загуба.
- Загуба на класификация за модел на класификация на ядрото на Гаус - загуба на MATLAB
- Класификация на затлъстяването, насочено към персонализирано диетично управление на загуба на тегло въз основа на
- Определете персонализиран претеглен класификационен слой - MATLAB; Simulink
- Определете персонализирани цикли за обучение, функции за загуба и мрежи - MATLAB; Simulink
- Дали често използваните модели на крехкост предсказват смъртност, загуба на автономност и умствен спад при по-възрастните