Оценете точността на научените тегла на характеристиките на тестовите данни
Синтаксис
грешка = загуба (mdl, X, Y)
грешка = загуба (mdl, X, Y, име, стойност)
Описание
err = загуба (mdl, X, Y) връща средната квадратична грешка като мярка за точност при грешка, за модела mdl, стойности на предиктор в X и стойности на отговор в Y .
err = загуба (mdl, X, Y, Name, Value) връща мярката за точност, err, с допълнителната опция, посочена от аргумента за двойка Name, Value.
Аргументи за въвеждане
mdl - Модел за анализ на съседни компоненти за регресия
FeatureSelectionNCARegression обект
Модел за анализ на компонент на квартал за регресия, посочен като FeatureSelectionNCARegression обект.
X - Променливи стойности на предиктор
n-by-p матрица
Прогнозни стойности на променливи, посочени като n-by-p матрица, където n е броят на наблюденията и p е броят на предикторските променливи.
Типове данни: единичен | двойно
Y - Стойности на отговора
числов реален вектор с дължина n
Стойности на отговора, посочени като числов реален вектор с дължина n, където n е броят на наблюденията.
Типове данни: единичен | двойно
Аргументи за двойка име-стойност
Посочете незадължителни двойки, разделени със запетая, на аргументи Name, Value. Name е името на аргумента, а Value е съответната стойност. Името трябва да се появи в кавичките. Можете да посочите няколко аргумента за двойка имена и стойност в произволен ред като Name1, Value1. NameN, ValueN .
'LossFunction' - Тип функция за загуба
'mse' (по подразбиране) | 'луд'
Тип функция за загуба, посочена като двойка, разделена със запетая, състояща се от „Функция за загуба“ и едно от следните.
| 'mse' | Средна квадратна грешка |
| 'луд' | Средно абсолютно отклонение |
Пример: 'LossFunction', 'mse'
Изходни аргументи
грешка - по-малка и по-добра мярка за точност на усвоените тегла на характеристиките
скаларна стойност
По-малка и по-добра мярка за точност на усвоени тегла на характеристиките, върната като скаларна стойност. Можете да посочите мярката за точност, като използвате аргумента LossFunction двойка име-стойност.
Примери
Настройте NCA модел за регресия Използвайки загуба и прогнозиране
Заредете примерните данни.
Изтеглете данните за корпуса [1] от хранилището за машинно обучение на UCI [2]. Наборът от данни има 506 наблюдения. Първите 13 колони съдържат предикторните стойности, а последната колона съдържа стойностите на отговора. Целта е да се предскаже средната стойност на обитаваните от собствениците домове в предградията на Бостън като функция на 13 предиктора.
Заредете данните и дефинирайте вектора на отговора и матрицата за предсказване.
Разделете данните в обучителни и тестови набори, като използвате 4-ти предиктор като променлива за групиране за стратифицирано разделяне. Това гарантира, че всеки дял включва подобно количество наблюдения от всяка група.
cvpartition разпределя на случаен принцип 56 наблюдения в тестов набор, а останалите данни в набор за обучение.
Извършете избор на функция, като използвате настройки по подразбиране
Извършете избор на функция, като използвате NCA модел за регресия. Стандартизирайте предикторните стойности.
Начертайте тежестите на характеристиките.
Теглото на неподходящите характеристики се очаква да се доближи до нула. fsrnca идентифицира две характеристики като ирелевантни.
Изчислете загубата от регресия.
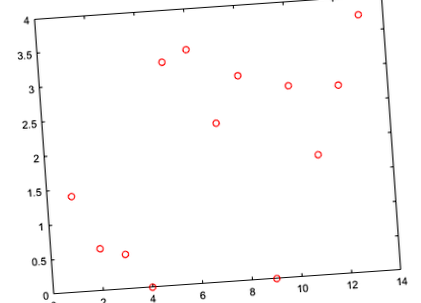
Изчислете прогнозираните стойности на отговора за тестовия набор и ги начертайте спрямо действителния отговор.
Перфектното прилягане спрямо действителните стойности образува права линия от 45 градуса. В този график прогнозираните и действителните стойности на отговора изглеждат разпръснати около тази линия. Настройката на стойност λ (параметър на регуларизация) обикновено помага за подобряване на производителността.
Настройте параметъра на регуларизация, като използвате 10-кратно кръстосано валидиране
Настройката на λ означава намиране на стойността на λ, която ще доведе до минималната загуба на регресия. Ето стъпките за настройка на λ с помощта на 10-кратна кръстосана проверка:
1. Първо разделете данните на 10 пъти. За всяко сгъване cvpartition присвоява 1/10 от данните като набор за обучение и 9/10 от данните като набор от тестове.
Задайте стойностите на λ за търсене. Създайте масив за съхраняване на стойностите на загубите.
2. Тренирайте модела за анализ на компонента на квартала (nca) за всяка стойност на λ, като използвате обучителния набор във всяка гънка.
3. Поставете модел на регресия на Гаус (gpr), като използвате избраните функции. След това изчислете загубата на регресия за съответния набор от тестове в гънката, използвайки модела gpr. Запишете стойността на загубата.
4. Повторете това за всяка стойност на λ и всяко сгъване.
Изчислете средната загуба, получена от гънките за всяка стойност на λ. Начертайте средната загуба спрямо стойностите на λ.
Намерете стойността на λ, която произвежда минималната стойност на загубата.
Извършете избор на функция за регресия, като използвате най-добрата стойност λ. Стандартизирайте предикторните стойности.
- Оценете точността на научените тегла на характеристиките на тестовите данни - MATLAB
- Загуба на класификация за модел на класификация на ядрото на Гаус - загуба на MATLAB
- Загуба на класификация за линейни класификационни модели - MATLAB
- Тест за чревни бактерии за отслабване Viome
- Мога ли да отслабна и тонус само с упражнения за плуване (мускули, вдигане на тежести) - Упражнение и