Субекти

Резюме

Въведение

Почвените информационни системи се използват все по-често за разработване на разбиране на екосистемния мащаб на критичните зонови процеси и екосистемните услуги 1,2. Съвсем наскоро по-голяма роля се приписва на широкомащабни данни за почвата за реализиране на целите за устойчиво развитие на продоволствената сигурност, управлението на водите и други заплахи за здравето 3. Използвани са изчерпателни бази данни за разработване на функции за педотрансфер (PTF) за критични параметри на почвата като хидравлични свойства на почвата (UNSODA 4, HYPRES 5), съдържание на органичен въглерод в почвата (SOC) (LUCAS 6) и геохимични параметри (GEMAS 7). По същия начин усилията за проучване на почвата доведоха до създаването на големи хранилища на стари бази данни за почвите в много страни. Напоследък данните за наследство за 196 498 геореферентни места, обхващащи 173 държави, бяха обединени, за да се създаде глобална почвена информационна система под шапката на Global Soil Partnership 8. Интересното е, че голяма част от данните за наследените почви остават до голяма степен недостатъчно използвани 9 .

Въпреки че PTF са привлекателни, тяхната надеждност зависи от количеството (размера на данните) и структурата на входните параметри 10,11. Например наборите от данни с няколко почвени проби може да са достатъчни за разработване на надеждни PTF за относително малки географски райони 12. Въпреки това, в голям и разнороден ландшафт с висока пространствена променливост на почвата 13, ефективността на PTF се влияе от размера и разпространението на местата за вземане на проби от почвата 14. Обикновено се твърди, че PTF не трябва да се екстраполират извън географския регион или типа на почвата, от който са разработени 15,16,17,18,19. Подобно предложение доведе до създаването на няколко специфични за региона и PTF бази данни за почвите в страни и континенти 4,5,6,7. В идеалния случай приликите или разликите между данните за калибриране и валидиране и основната структура на корелация следва да се разглеждат като ключови детерминанти за ефикасността на разработения PTF 20,21, а не за техния географски произход. Подобна хипотеза не е тествана с експериментални данни, доколкото ни е известно. По-конкретно, какво представлява ключовите компоненти на набор от данни за обучение и как да се генерира такъв набор от данни не са ясно дефинирани.

Пространствената променливост в почвите е сложна и свойствата на почвата обикновено не следват правилата за пространствена стационарност 22. Освен това много свойства на почвата в проби, събрани от големи площи, показват присъщи нелинейности 14. Наследените данни за почвата също така съдържат информация както за пространствената променливост, така и за нелинейността 23. Освен това размерът и обемът на данните, налични в много стари бази данни за почвите, са големи 24. По този начин наследените данни могат да служат като богат източник на данни за разработване на специфични за региона PTF, ако ключовите характеристики на набора от данни за обучение са добре дефинирани и е разработена методология за извличане на такъв набор от наследени данни. Важно е, че подобна методология ще спести време и усилия, необходими за създаването на нови масиви от данни за разработване на специфични за региона PTF.

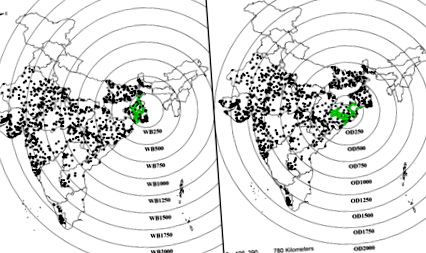
Следователно общата цел на това проучване беше да се изследва дали широкомащабните стари бази данни на почвите могат да се използват за получаване на данни за обучение за калибриране на PTF. Специфичната цел беше да се изследва как структурата на корелация, пространствената променливост и нелинейността в наборите от данни за обучение и тестове влияят върху ефективността на PTF. За да тестваме тези цели, ние избрахме данните от проучването на почвата, събрани от Националното бюро за проучване на почвите и планиране на земеползването (NBSS & LUP), Нагпур, Индия (оттук нататък, наричано индийско наследство на почвата или база данни ISL) като източник на наследени данни. Използвахме базата данни ISL (показана с черни точки на фиг. 1) за разработване на множество набори от данни за обучение за калибриране на PTF. През последното десетилетие разработихме и бази данни за почвите за щатите Одиша и Западна Бенгалия (показани със зелени точки на фиг. 1) като част от изграждането на спектрална библиотека за източноиндийски почви 25,26. Тези две регионални бази данни за почвите бяха използвани като независими набори от тестови данни; оттук нататък тези бази данни се наричат ​​тестови данни от Западна Бенгалия (база данни на WBT) и данни от тестове на Odisha (база данни ODT). Тъй като данните за капацитет за обмен на катиони (CEC) бяха налични във всичките три набора от данни и това е важен параметър 27 на почвената функция, ние избрахме CEC като кандидат за разработване на PTF от наследена база данни. Както линейни, така и нелинейни подходи за моделиране като множествена линейна регресия (MLR), регресия на хребета (RR), регресия на подпомагащи вектори (SVR), случайна гора (RF) и усилване на екстремен градиент (XGB) бяха изследвани, за да се разработи стабилна PTF за ЦИК. Подходът XGB е ефективен алгоритъм за машинно обучение 28 и не е използван за разработване на PTF в почвената литература.

нелинейност

Карта на Индия с местата за вземане на проби за данните от наследството на индийската почва. Девет набора от данни за местоположението на почвата (WB250 до WB2250) бяха получени чрез изчертаване на кръгове с посочени радиуси 250–2,250 km от централната точка (88.901 ° E и 23.126 ° N), разположена в Западна Бенгалия (десен панел). Осем набора от данни за местоположението на почвата (OD250 до OD2250) бяха получени чрез изчертаване на кръгове с посочени радиуси 250–2000 km от централната точка (85.584 ° E и 21.088 ° N), разположена в щата Одиша (ляв панел). Местата за вземане на проби за тестове от Западна Бенгалия (WBT) и Одиша (ODT), събрани от лабораторията по физика на почвата в Индийския технологичен институт Харагпур, Индия, са показани като зелени точки.

База данни за наследство на индийски почви (данни за обучение)

База данни на Западна Бенгалия и Одиша (тестови данни)

Избор на данни за обучение от мащабна база данни за наследство на почвата

Локално сходство

Пространствена структура в данните за обучение и тестове

Пространствена променливост в данните от теста

Наборът от данни за WBT доведе до линейна полувариограма за CEC с единица = 32,13, перваз = 52,38 и обхват = 24,45 км, докато данните за ODT показват чиста самородна вариограма (единица = 105,18). Повторихме анализите на полувариограмата, като премахнахме тенденцията в данните от CEC за пробите от WBT и резултатите показаха чист зародиш ефект, подобен на ODT набора от данни. Без пространствена структура, стойностите на CEC в тестовите набори от данни могат да се считат за произволно разпределени по тестовите зони.

Пространствена променливост в данните за обучение

Подобно на тестовите набори от данни, ние премахнахме тенденциите от всичките 34 набора от данни за обучение, преди да поставим полувариограми. Като цяло, сферичен модел е монтиран на остатъците от CEC, глината и стойностите на рН, докато експоненциален модел е монтиран на остатъците от стойностите на SOC. Стойностите на диапазона за полувариограмите, монтирани на всяко от свойствата на почвата за всеки от наборите от данни за обучение, са нанесени като функция от радиуса на набора от данни за обучение (Фиг. 2). Фигура 2 показва, че наборите от данни за обучение имат стойности на обхват от около 1250 km за CEC, 1000 km глина и около 1500 km за стойности на pH и SOC. С параметъра на обхвата, вариращ от 1 000–1 500 км, може да се очаква да има пространствено корелиран отговор и променлива на предиктора, дори ако използваме цялата база данни ISL като набор от данни за обучение. Получени вариограми, получени за набори от данни за повърхностни почви, ориентирани към Западна Бенгалия, и набори от данни за обучение за ориентиране в Odisha за цели профилни почви са показани за илюстрация като допълнителен материал (фиг. S3).

Диапазони (km) за теоретичните полувариограми, съобразени с капацитета за обмен на катиони (CEC), глината, рН и органичния въглерод в почвата (SOC) за всеки набор от данни за местоположението в Западна Бенгалия (WB) и Одиша (OD) спрямо радиусите (km) за всеки от тези набори от данни за местоположение.

Структура на корелация между предиктор и променливи на отговора

Коефициент на корелация на Pearsons и стойности на коефициента на корелация на разстоянието между капацитет на обмен на катиони (CEC) и съдържание на глина (глина), CEC и pH, CEC и съдържание на органичен въглерод в почвата (SOC) и CEC и глина, pH, SOC, комбинирани за Западна Бенгалия наследени набори от данни за местоположението за пробите на целия профил на почвата.

PTF за CEC от стари данни

Максимални коефициенти на корелация на Pearsons (ρ) спрямо минималните стойности на средноквадратична грешка (RMSE) за PTFs, тествани в наборите от тестове за Западна Бенгалия и Одиша, обучени на специфичните набори от данни за обучение, които показват максималния ρ. Фигурата също така нанася максималните коефициенти на корелация на разстоянието (dCor) спрямо минималните стойности на средноквадратична грешка (RMSE) за PTFs, тествани в наборите от тестове за Западна Бенгалия и Одиша, обучени на специфичните набори от данни за обучение, които показват максималните стойности на dCor.

Дискусия

Следвана схема за използване на наследените данни за почвата за получаване на специфични за региона стабилни функции на педотрансфера за трудно измерими свойства на почвата; GAM: общ модел на добавка, dCor: корелация на разстояние, CEC: катионообменна способност, SOC: съдържание на органичен въглерод в почвата.

Методи

M1-събиране и компилация на набор от тестове

M2-избор на набори от данни за обучение

М3-геостатистически анализ

Проучихме пространствената структура във всички набори от данни за обучение и набори от тестови данни за всички свойства на почвата, участващи в разработването на PTF. За целите данни за почвения профил, среднопретеглената стойност на данните за почвения профил е взета за всяко място за оценка на полувариограмите. Различни теоретични функции на полувариограмите бяха монтирани на всяка от тези експериментални полувариограми, за да се получат стойностите на обхвата, късчето и перваза. Тези параметри осигуряват средна мярка за различие за свойство като функция на разстоянието на разделяне. Избрани са най-добре монтираните теоретични модели на полувариограми въз основа на претеглено фитинго с най-малък квадрат, където теглата (wi) за всеки клас изоставане са пропорционални на броя двойки данни и обратно пропорционални на разстоянието на изоставане. Тъй като пробите от почвата бяха събрани от широки географски райони, премахнахме стационарността в наборите от данни, преди да поставим моделите на полувариограмата. Моделът на повърхността на тенденцията беше монтиран, за да отклони наблюдаваните данни, използвайки подход с най-малък квадрат. След това остатъците (= разлика между наблюдавания и моделирания параметър на почвата) бяха използвани за оценка на полувариограмите. Всички геостатистически анализи бяха извършени с помощта на решетка и gstat пакети в среда за програмиране R 51 .

Измервания на зависимостта M4

Използван е и подход на обобщено адитивно моделиране (GAM) 52, за да се изследва пределната връзка между стойностите на CEC и прогностичната променлива (и), като pH, съдържание на глина и SOC. Основната идея в GAM е да се побере функция на всеки от предикторите, за да улови връзките между реакцията и променливите на предиктора. Ефективните степени на свобода на изглаждащия сплайн, монтиран на всяка от променливите на предиктора, е индикация за основната нелинейност между предикторите и променливата на отговора. Използва се наказателен изглаждащ сплайн подход, за да се изберат ефективните степени на свобода за изглаждащите сплайни за това проучване, като се използва mgcv пакет в среда за програмиране R 51 .

Използвахме както линейни, така и нелинейни корелационни мерки за количествена оценка на степента на корелация между различните почвени параметри. Коефициентът на корелация на Pearson (ρ), описващ линейната корелация между два параметъра, е даден като:

където х и у са две случайни променливи и н е броят на променливите. По същия начин, корелацията на разстоянието 53 (dCor) е нелинейна мярка за зависимост, основана на функции на разпределение или плътност и се дава като: