Блогпост от Павел Измайлов, Тимур Гарипов и Андрю Гордън Уилсън; визуализации в сътрудничество Javier Ideami.

загуба

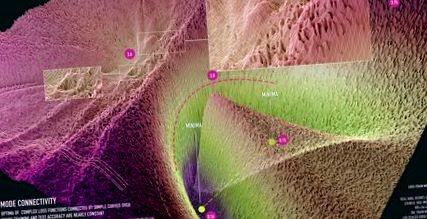
Фигура 1: визуализация на свързаност в режим за ResNet-20 без пропускане на връзки в набора от данни CIFAR-10. Визуализацията е създадена в сътрудничество с Хавиер Идеями (https://losslandscape.com/).

Разбирането на обобщаването в дълбоките невронни мрежи е чудесен отворен въпрос. Невронните мрежи се обучават чрез минимизиране на повърхностите на загуби, които са силно мултимодални, с много настройки на параметри, които не постигат загуба на обучение, но лошо обобщение. Разбирайки геометричните свойства на тези повърхности на загуби, можем да започнем да решаваме тези въпроси и да изграждаме по-ефективни тренировъчни процедури. Всъщност, локалната гладкост и изпъкналост на повърхностите на загубите се използва за анализ на конвергенцията на SGD и други оптимизатори [напр. ж. 12]. Наскоро беше предложено стохастично усредняване на теглото [5], за да се намерят по-плоски области на загубата, което води до по-добро обобщение.

Формата на повърхността също има голямо значение за байесовите подходи в дълбокото обучение. С байесов подход ние не само искаме да намерим една точка, която оптимизира риска, а по-скоро да се интегрираме върху повърхността на загубите, за да формираме средна стойност на байесов модел. Следователно геометричните свойства на повърхността на загубите, а не конкретните местоположения на оптима, оказват значително влияние върху прогнозното разпределение при байесова процедура. Съответно, последните подходи използват геометрията на траекторията на SGD за мащабируеми и високоефективни процедури на байесов извод [6, 7].

Все още знаем много малко за свойствата на тези повърхности на загуби. Правят се нови открития, показващи топологично поведение, силно отличаващо се от невронните мрежи. В тази публикация в блога описваме свързаност на режима, изненадващо свойство на съвременните пейзажи на невронни мрежи, представени в нашата статия NeurIPS 2018. Изложението ни в тази публикация се фокусира върху получаването на интуиция чрез визуализация.

Обикновено локалните оптимуми на дълбоките невронни мрежи се представят като изолирани басейни, както е в левия панел на фигура 2. На тази фигура ние визуализираме повърхността с големи размери на загубите в равнината, образувана от всички афинни комбинации от три независимо обучени мрежи. В следващия раздел описваме подробностите за процедурата за визуализация. Тази интуиция идва от следния експеримент: ако обучим две мрежи с една и съща архитектура, получаваме две различни локални оптимуми в пространството на параметрите; загубата по линейния сегмент, свързващ двете решения, се взривява между оптимите, достигайки стойности, постигнати от напълно нетренирани мрежи при инициализация. Изненадващо, оптимите всъщност не са изолирани. Можем да намерим извита пътека между тях, така че загубата да бъде ефективно постоянна по пътя. Ние наричаме това явление като свързаност на режима. Тези извити пътища могат да бъдат много прости, като тези, показани в средния и десния панел на Фигура 2. Тези пътища също са лесни за намиране, както обясняваме по-долу.

Фигура 2: Загубена повърхност на ResNet-164 на CIFAR-100. Наляво: три оптими за независимо обучени мрежи; Средна и Нали: Квадратична крива на Безие и многоъгълна верига с един завой, свързващ долните две оптими в левия панел по път с почти постоянна загуба.

Доказано е, че свързаността на режима се държи много общо. В режим [1, 2] се демонстрира свързаност за множество модерни архитектури за класификация на изображения и някои повтарящи се архитектури върху текстови данни. В [3] авторите показват, че е възможно да се свържат оптими, обучени с различни оптимизатори и хипер-параметри, като размери на партиди, намаляване на теглото, график на скоростта на обучение и стратегия за увеличаване на данните. В [4] авторите, че свързаността на режима се поддържа за алгоритмите за оптимизиране на политиките при задълбочено обучение за подсилване.

Как да визуализираме загубени повърхности?

Визуализацията ни помага да анализираме и изградим интуиция за сложни обекти. Визуализациите, базирани на намаляване на размерите, могат да разкрият интерпретируема структура, което води до нови научни прозрения; например, в [11] t-SNE визуализациите са използвани за откриване на нови подтипове ретинални клетки. Тук ние изучаваме свойствата на функциите на загуба на дълбоките невронни мрежи, които зависят от милиони (или понякога дори милиарди!) Параметри. Не можем директно да визуализираме милионномерна повърхност. Въпреки това, можем да разгледаме 2D фрагмент от функцията за загуба и ако този фрагмент е избран внимателно, той може да даде представа за структурата на пейзажа.

Фигура 3: Илюстрация на процедурата за визуализация на повърхността на загубите. Избираме 2D равнина в пространството на параметрите на невронна мрежа, изграждаме координатна система в равнината и дефинираме мрежа в тази координатна система. След това оценяваме загубата за всяка точка в мрежата и визуализираме резултата.

Три точки в пространството на параметрите винаги определят уникална 2D равнина, която преминава през тези точки. Да предположим, че имаме три точки \ (w_1, w_2, w_3 \) в пространството за тежести. Това могат например да бъдат векторите на параметри (всички тегла и отклонения, свързани в един вектор) на три независимо обучени мрежи, както в левия панел на Фигура 2. Можем да изградим двумерна равнина, минаваща през \ (w_1, w_2, w_3 \), както следва. Определяме основа за равнината да бъде \ (u = (w_2-w_1), v = (w_3-w_1) \) и вектора на изместване да бъде \ (w_1 \). Можем да ортогонализираме основата, като превключим на \ (v = v - cos (u, v) u \), където \ (cos (u, v) \) е косинусът на ъгъла между векторите \ (u \) и \ (v \). След това можем да дефинираме декартова координатна система в равнината и да картографираме \ ((x, y) \) координати към точките в оригиналното пространство на параметрите, използвайки формулата \ (w (x, y) = w_1 + u \ cdot x + v \ cdot y \). Сега можем да изградим мрежа в координатната система и да оценим функцията на загуба за мрежата, съответстваща на всяка от точките в мрежата, и да визуализираме резултатите. Фигура 3 илюстрира процеса на визуализация.

Намиране на пътища между режимите

Методът за намиране на път с ниски загуби между двойка оптима е интуитивно много прост: ние параметризираме пътя и минимизираме средната загуба по пътя по отношение на неговите параметри. Да приемем формално, че имаме две оптими \ (w_1 \) и \ (w_2 \) на функцията за загуба. След това дефинираме път, който ги свързва като \ (\ phi (t) \), преобразуване от сегмента \ ([0, 1] \) в пространството на параметрите, така че \ (\ phi (0) = w_1, \ phi (1) = w_2 \). Например можем да използваме квадратна крива на Безие: \ (\ phi (t) = (1 - t) ^ 2 w_1 + 2t (1-t) \ theta + t ^ 2 w_2 \), показана с черна линия в средният панел на Фигура 2. Тук е параметърът на кривата, който има същата размерност и структура като векторите на тежестта \ (w_1 \) и \ (w_2 \). Ние тренираме, за да сведем до минимум средната загуба по кривата. По-конкретно, ние свеждаме до минимум

по отношение на \ (\ theta \), където \ (Loss () \) е стандартната функция за загуби, използвана за обучение на мрежите \ (w_1 \), \ (w_2 \), като загуба на кръстосана ентропия за класификация.

Можем ефективно да изчислим стохастични градиенти на \ (L (\ theta) \) по отношение на \ (\ theta \). За целта вземаме проба от точка \ (t \) равномерно върху \ ([0, 1] \) и след това изчисляваме градиента на \ (Загуба (\ phi (t)) \) по отношение на \ (\ theta \) използвайки правилото на веригата:

Използвайки тази стохастична оценка на градиента, ние намаляваме \ (L (\ theta) \) със стандартен SGD.

За квадратната крива на Безие целият път \ (\ phi (t) \) се намира в двумерно подпространство на пространството на параметрите. Можем да визуализираме функцията за загуба в тази равнина по време на обучението, като използваме процедурата за визуализация, описана в предишния раздел.

Визуализации с висока разделителна способност на свързаност в режим

В сътрудничество с Javier Ideami наскоро създадохме визуализации с висока разделителна способност на повърхностите на загубите в равнините, съдържащи режим на свързаност. Създадохме видео, показващо тренировъчния процес на квадратична крива на Безие, свързваща двойка локални оптими за ResNet-20 без връзки за пропускане на CIFAR-10:

Във видеото оптимите преминават от изолиране и изключване за произволно инициализирана крива към свързване чрез тунел с ниски загуби, както е показано на фигура 1.

Също така създадохме статични визуализации на ResNet-20 на набора от данни FastAI Imagenette с още по-висока разделителна способност 1000x1000. Ние показваме тези визуализации на фигури 4, 5, 6.

Фигура 4: Визуализация на свързаност в режим за ResNet-20 без пропускане на връзки в набора от данни на ImageNet. Визуализацията е създадена в сътрудничество с Хавиер Идеями (https://losslandscape.com/).

Фигура 5: визуализация на свързаност в режим за ResNet-20 без пропускане на връзки в набора от данни на Imagenette. Визуализацията е създадена в сътрудничество с Хавиер Идеями (https://losslandscape.com/).

Фигура 6: визуализация на свързаност в режим за ResNet-20 без пропускане на връзки в набора от данни на Imagenette. Визуализацията е създадена в сътрудничество с Хавиер Идеями (https://losslandscape.com/).

На уебсайта на Javier https://losslandscape.com/ можете да намерите други артистични визуализации с висока разделителна способност на повърхностите на загуба на невронна мрежа, както статични, така и динамични.

Изчислителни разходи за създаване на визуализации

За всяка от визуализациите изчисляваме загубата за всяка точка в мрежа (съответстваща на различна настройка на мрежовите тегла). За фигури 4, 5, 6 използвахме мрежа 1000x1000, която изисква оценка на загубата за невронна мрежа при милион различни настройки на нейните параметри. За видеото изчислихме 600 кадъра с разделителна способност 300x300, което възлиза на над 50 милиона оценки на загубите. За да ограничим изчислителните разходи, използваме поддискретизирана версия на набора от данни, като се уверим, че тази поддискретизация запазва структурата във визуализации. Дори и с по-малкия набор от данни, процесът на визуализация на видеото отне повече от две седмици, използвайки 15 графични процесора. Създаването на статични визуализации с висока разделителна способност на фигури 4, 5, 6 отне около два дни с помощта на три графични процесора.

Дали тези пътеки съдържат различни представяния?

Известно е, че параметризацията на невронните мрежи съдържа дегенерации. Например в мрежите ReLU можем да умножим теглата в един слой с определена стойност и да разделим теглата в следващия слой със същата стойност и изходите на мрежата (и следователно загубата) няма да се променят. По този начин е естествено да се запитаме дали свързаността на режима съществува само поради такива дегенерации при параметризацията. Вместо това откриваме, че пътищата с ниски загуби съдържат богата колекция от различни представления, предоставящи различни прогнози за тестови данни. Демонстрираме разнообразието от функции по пътя на ниски загуби за 1D регресионен проблем на Фигура 7.

Фигура 7: Загубена повърхност в 2D равнината, съдържаща пътека с ниски загуби (вдясно) и функциите за предсказване, съответстващи на различни точки в тази равнина (вляво) за DNN, обучен по 1D регресионен проблем. Различните точки по кривата, показани с пурпурни кръгове вдясно, съответстват на различни функции, показани с пурпурни линии вляво. Моля, вижте [7] за подробно описание на този експеримент.

Всъщност кривите свързват двойка различни оптими \ (w_1 \) и \ (w_2 \), които създават различни прогнози. Следователно прогнозите трябва да се променят по някакъв начин по кривата. Можем да проверим, че прогнозите на мрежите по пътя \ (\ phi \) са съществено различни, като разгледаме работата на ансамблите от тези мрежи. Разглеждаме ансамбли от две мрежи: едната е фиксирана на \ (w_1 \), а другата \ (\ phi (t) \) се движи към \ (w_2 \) по пътя \ (\ phi \). Установяваме, че ансамбълът от \ (w_1 \) и \ (\ phi (t) \) се представя, както и ансамбълът от независимо обучени \ (w_1 \) и \ (w_2 \), дори за \ (t \ приблизително 0,3 \ ), което предполага, че мрежите по пътя са съществено различни от крайните точки. Визуализираме представянето на ансамбъла като функция от точката на кривата на Фигура 8.

Фигура 8: Изпълнение на ансамбъла от крайна точка на пътя и точка от пътя като функция на точката на пътя. За сравнение визуализираме изпълнението на ансамбъла за сегмента на директната линия, свързващ optima, както и за пътя, научен по нашия метод.

Нова работа

Има няколко статии, които предоставят теоретични обяснения на свързаността на режима. Например, неотдавнашната статия [4] демонстрира, че различните понятия за стабилност на шума, като стабилност до отпадащи смущения, предполагат свързаност на режима. Документи [8, 9] предоставят различни теоретични перспективи за свързаност на режима, като показват, че при определени предположения всички поднива на набора от загуба на DNN са свързани.

Свързването на режима вдъхнови нови практически методи за обучение на невронни мрежи с подобрено обобщение и количествено определяне на несигурността. На високо ниво свързаността на режима показва, че е възможно да се пътува между различни режими на функцията за загуба, без да се оставя общ регион с ниски загуби. Стохастично усредняване на теглото (SWA) [5] използва тази идея и изследва разнообразни решения около дадено решение, като стартира SGD с висока постоянна скорост на обучение; след това се усредняват итерациите на SGD от различни епохи, за да се получи ново решение със значително подобрено обобщение. SWA-Gaussian [6] разширява SWA, за да улови също ковариацията на SGD итерации и конструира гауссово разпределение върху тежестите; чрез вземане на проби от това разпределение за формиране на средна стойност на байесов модел е възможно значително да се подобри както точността на модела, така и представянето на несигурността, в сравнение със стандартния SGD. И накрая, [7] апроксимира Байесовата задна част над тежестите на мрежа в подпространството, съдържаща пътека с ниски загуби между оптимите и извършва усредняване на Байесов модел, използвайки това приближение.

Неотдавнашната статия [10] разширява нашия метод за намиране на криви с ниски загуби, за да се намерят равнини, където повърхността на загубите прилича на дадена картина. Изненадващо те успяха да намерят такива самолети за всяка снимка, която използваха. Ние показваме някои от техните примерни повърхности на загуби на Фигура 9. Фактът, че простият SGD може лесно да намери тези сложни структури в повърхността на загубите, загатва за благословия на размерността. Високата размерност на пространството на параметрите осигурява много пътища към добри решения.

Фигура 9: визуализация на загубите в равнини, конструирани в [10] за набори от данни FashionMNIST и CIFAR-10. Тази цифра се копира директно от [10].

Препратки

[1] Загуба на повърхности, свързване на режима и бързо сглобяване на DNN; Тимур Гарипов, Павел Измайлов, Дмитрий Подоприхин, Дмитрий Ветров, Андрю Гордън Уилсън; Системи за невронна обработка на информация (NeurIPS), 2018

[2] По същество няма бариери в енергийния пейзаж на невронната мрежа; Феликс Дракслер, Камбис Вешгини, Манфред Салмхофер, Фред А. Хампрехт; Международна конференция по машинно обучение (ICML), 2018.

[3] По-подробен поглед към евристиката на задълбоченото обучение: Скоростта на обучение се рестартира, загряване и дестилация; A. Gotmare, N. Keskar, C. Xiong & R. Socher; Международна конференция за учебни представителства (ICLR) 2019

[4] Разбиране на въздействието на ентропията върху оптимизацията на политиката; Zafarali Ahmed, Nicolas Le Roux, Mohammad Norouzi, Dale Schuurmans; Международна конференция за учебни представителства (ICLR) 2019

[4] Обяснение на пейзажната свързаност на евтини решения за многослойни мрежи; Rohith Kuditipudi, Xiang Wang, Holden Lee, Yi Zhang, Zhiyuan Li, Wei Hu, Rong Ge, Sanjeev Arora; Системи за невронна обработка на информация (NeurIPS), 2019

[5] Средното тегло води до по-широка оптима и по-добро обобщение; Павел Измайлов, Дмитрий Подоприхин, Тимур Гарипов, Дмитрий Ветров, Андрю Гордън Уилсън; Несигурност в изкуствения интелект (UAI), 2018

[6] Просто изходно ниво на несигурността на Байес при задълбочено обучение Уесли Мадокс, Тимур Гарипов, Павел Измайлов, Дмитрий Ветров, Андрю Гордън Уилсън Невронни системи за обработка на информация (NeurIPS), 2019

[7] Подпространствено заключение за Байесово дълбоко обучение; Павел Измайлов, Уесли Дж. Мадокс, Полина Кириченко, Тимур Гарипов, Дмитрий Ветров, Андрю Гордън Уилсън; Несигурност в изкуствения интелект (UAI), 2019

[8] За свързаните поднивови набори в дълбокото обучение; Куин Нгуен; Международна конференция по машинно обучение (ICML), 2018.

[9] Топология и геометрия на полуректифицирана мрежова оптимизация; В. Даниел Фрийман, Джоан Бруна

[10] Загуба на пейзаж с многоточково оптимизиране; Иван Скороходов, Михаил Бурцев, 2019

[11] Силно паралелно геномно експресиране на отделни клетки с помощта на нанолитрови капчици