Всичко във Вселената, което има маса, има гравитация. В Лесно е да се разбере, че Земята, каквато и да е, има гравитация, която ни дърпа постоянно, задържайки ни на Terra Firma. В Също толкова лесно е да се разбере, че други големи обекти имат гравитация, като Луната, планетите и Слънцето.
Обаче е много по-трудно да се разбере, че всеки човек на Земята има гравитация. Странно е, че упражнявате сила върху Земята и върху всеки друг човек. В Вие също упражнявате сила върху всяка скала, дърво и същество, които бродят по Земята, и всички те упражняват сила върху вас. В Единственият проблем е, че имате толкова малка маса в сравнение със Земята, гравитационната сила, която упражнявате, е много малка.
Когато обяснявам тази идея, често ме питат „Защо не усещаме гравитацията от планина?“
Първо, това е така, защото самата Земя тежи много повече от планината, така че планината има малка гравитация, въпреки че е огромна. В Другата причина е, че гравитацията, упражнявана от която и да е сферично разпределена маса (като Земята), се държи така, сякаш цялата маса е в центъра на обекта. В Ако искате да видите действителната математика, проверете тази връзка за разбивка.
Ако планината не може да упражни достатъчно сила, за да се почувстваме, какво ще кажете за Луната? Луната е голяма и е относително близо до нас. Ами ако Луната е отгоре? Дали това ще ни направи по-леки? Щеше ли да ни направи по-тежки, ако беше в далечната страна на Земята?
Нека разберем!
Исак Нютон първо разбра силата на гравитацията и как действа тя. В Той излезе с уравнение за измерване на гравитационната сила между всеки два обекта:
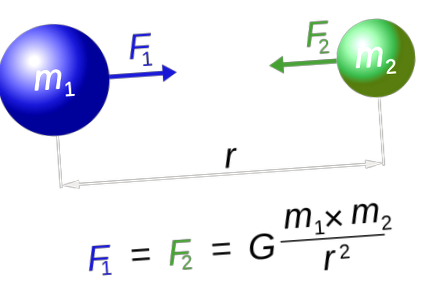
Където r е разстоянието между центъра на масата на обектите, а G е универсалната гравитационна константа, където G = 6,67 x 10 -11 N (m/kg) 2 .
Ти, стоящ на Земята!
Земята тежи 5,72 × 10 24 Kg, а разстоянието между вас и центъра на Земята (където усещате привличането на гравитацията) е r = 6 371 000 m. В Хвърлете всичко това в уравнението по-горе и ние откриваме, че силата, упражнявана върху вас от Земята, е:
9.4 пъти масата ви. В Ето защо по-масивните неща са по-трудни за вдигане. В Действителният отговор, измерен чрез висококачествени експерименти, е 9,81 пъти вашата маса. В Това е различно от нашето изчисление, поради факта, че Земята няма точно еднаква плътност навсякъде (част от нея е вода, скали и т.н.). В Ако разделите тази сила на вашата маса, получавате ускорението на Земята поради гравитацията, независимо от масата:
Всички неща се ускоряват с еднаква скорост, независимо колко тежки са. В перо пада толкова бързо, колкото топка за боулинг. Единствената разлика е, че топката за боулинг ще боли много повече, ако падне върху вас.В
Сега Луната
Земята и Луната обикалят около точка около тях, техния център на масата. В Тъй като Земята е по-масивна, центърът на масата на системата Земя-Луна е вътре в Земята, на около 1700 км под повърхността. В Това означава, че Земята се „клатушка“, докато Луната обикаля.
Кредит за изображение: Rnt20 Wikipedia CC 3.0
Земята и Луната всъщност са в свободно падане около този център на масата. В Същото е като астронавтите в космически кораб, обикалящ около Земята. В Те падат около Земята в елипса, но без неподвижна повърхност, която да ги бута, те се чувстват безтегловни. В тяхната нетна сила е центростремителната сила, която е равна на гравитационната сила. В Центробежната сила се дава от:
И вие, и Земята сте в свободно падане около центъра на масата. В Но тъй като сте неподвижни на Земята, земята ви натиска и вие възприемате земната гравитация.
"Но мислех, че приливите в океана се случват поради гравитацията на Луната!"
Те правят! Когато говорим за взаимодействието на две големи тела, като гравитационното влияние на Луната върху Земята, трябва да обсъдим приливната сила.
Тъй като Земята е голямо твърдо тяло, тя се движи по цялата маса с еднаква скорост. В Това е ключът към приливните сили. Центропеталната сила на Земята е една и съща по целия си диаметър, но тъй като гравитацията зависи от разстоянието, страната на Земята, обърната към Луната, усеща повече гравитация, отколкото страната, обърната настрани. В Това води до приливна сила от двете страни на Земята, насочена встрани от центъра.
Това означава, че В. вие тежите по-малко, когато Луната е над вас И когато Луната е на противоположната страна на Земята от вас. В И в двата случая теглото ви се променя с (почти) същото количество. В Ето карта на приливната сила от различни точки по земната повърхност.
Кредит: Итън Сийгъл http://scienceblogs.com/startswithabang
И така, колко силна е приливната сила? Колко се променя теглото ни заради Луната?
(Забележка: Ако не искате да виждате математиката, превъртете надолу, за да видите отговора)
За да намерим приливната сила В от Луната, ще сравним ускорението на Луната поради гравитацията, действаща на ръба на Земята, с това в центъра на Земята. В Тъй като сме свързани със Земята, имаме точно същата центростремителна сила и затова трябва да усетим приливната сила, която действа и върху нас.
За страната, обърната към Луната:
Тъй като Force = Mass x Acceleration, можем да вземем закона на Нютон за гравитацията отгоре и да разделим двете страни на маса, за да получим следната формула за ускорение поради гравитацията.
aВ = G * В MВ/r 2
За ръба на Земята в този случай r ще бъде разстоянието Земя-Луна (което се измерва от центъра на Земята до центъра на Луната) минус радиуса на Земята. В Когато правим изчислението за далечната страна, ще добавим радиуса на Земята към разстоянието Земя-Луна.
Така че, ако разстоянието Земя-Луна е R, а радиусът на Земята е rEarth,
anear В = G * В Mmoon/(R - r Earth) 2 В - G * В Mmoon/R 2
Разстоянието Земя-Луна е приблизително 380 000 000 m, радиусът на Земята е 6 371 000 m, G е G = 6,67 x 10 -11 N (m/kg) 2, а Луната има маса 7,348 x 10 22 Kg. В Изчислението ни дава:
навън В = 0,00000117 m/s 2
Много малко ускорение.
За страната срещу Луната:
Този път за ръба на Земята r ще бъде разстоянието Земя-Луна плюс плюс радиусът на Земята. Използвайки същото уравнение като последния път с новите разстояния и изваждайки гравитацията В на ръба от това в центъра:
отдалеч В = G * В Mmoon/R 2 В –В G * В Mmoon/(RВ + r Земя) 2
Със същите числа като преди, изчислението ни дава:
отдалече В = 0,00000111 m/s 2
Малко по-малко ускорение.
Така приливната сила е малко по-силна от страна на Луната, но само с около 5%. В Нека сега сравним това с ускорението, дължащо се на гравитацията на Земята отгоре, 9,81 m/s 2 .
Гравитацията, която усещате от Луната, е малко над 1 милионна част от гравитацията, която усещате от Земята, което означава, че ако Луната е над главата ви или от противоположната страна на Земята, теглото ви ще спадне само с една милионна част от килограма.
Сега е съвсем очевидно, че гравитацията на Луната няма да даде и най-малък забележим ефект, а тъй като Слънцето и другите планети са много по-далеч, ефектът им също е малък. В Гравитацията на Слънчевата система просто не ни влияе, защото гравитацията намалява с квадрата на разстоянието. В Нещо, което е два пъти по-далеч от Земята, усеща само 1/4 от гравитацията. Така че нека го увеличим малко. В Има ли място в Слънчевата система, където да забележим разлика?
За тази ще пътуваме до Луната на Юпитер Йо. В Йо е най-близката от Галилеевите луни, а Юпитер е най-масивната планета в Слънчевата система. В Ще получим ли различен резултат?
Отново приливната сила ще ни направи по-леки, ако Юпитер е отгоре или от противоположната страна, точно както при Земята и Луната, но ще има ли забележима разлика?
Използвайки Юпитер, най-голямата планета в Слънчевата система, и Йо, най-близката му Луна, приливите и отливите на Юпитер ще ни направят по-леки?
Ще използваме същото уравнение, както преди, тъй като законът за гравитацията и приливните сили на Нютон се прилагат за почти всичко във Вселената (с изключение на може би лудите неща като черни дупки).
Този път масите са различни, както и разстоянията. В Ще разгледаме колко тежим на Io и колко е приливната сила. В Започнете с общата информация, от която ще се нуждаем:
Маса на Io = 8,93 x 10 22 Kg
Маса на Юпитер = 1,889 х 10 27 В кг
Радиус на Io = 1 821 600 m
Разстояние от Юпитер до Йо (център до центъра) = R = 421 700 000 m
1. Ускорение поради гравитацията В върху Io
Да забравим за секунда Юпитер и да видим какво е ускорението поради гравитацията на Io:
Използването на радиуса и масата на Io отгоре ни дава:
Йо има много по-малко гравитация от Земята, тъй като тя е много по-малка. Бихте тежали около 1/6 от теглото си на Земята (подобно на Луната всъщност).
2. Приливна сила поради гравитацията на Юпитер
Отново ще разгледаме близките и далечните страни на Йо, точно както направихме, когато стояхме на Земята. В Само този път могъщият Юпитер създава приливите и отливите.
За страната с Юпитер над нас:
Точно както при Земята и Луната, ще трябва да намерим разликата между гравитацията на ръба и гравитацията в центъра, така че използваме:
anear В = G * В MJup В/(R - r Io) 2 В - G * В MJup В/R 2
Където R е разстоянието между Йо и Юпитер. В Изчислявайки, получаваме:
навън В = 0,0062 В m/s 2
За страната срещу Юпитер:
Този път, както и преди, добавяме радиуса на Io към разстоянието Юпитер-Йо, за да получим правилната мярка на приливите и отливите:
далеч В = G * В MJup В/R 2 В - G * В MJup В/(R + r Io) 2
Където R е разстоянието между Йо и Юпитер. В Изчислявайки, получаваме:
навън В = 0,0061 В m/s 2
Много интересен резултат!
Това означава, че дори при мощната гравитация на Юпитер, теглото ви върху Йо ще варира само с един десет хиляда килограм!
Това е така, защото приливната сила наистина зависи от разстоянието между обектите. В Тъй като предметите се сближават, приливните сили се увеличават значително! В Ако Луната беше два пъти по-близо до нас, отколкото е сега, приливните сили, които тя упражнява върху Земята, биха се увеличили с 8 пъти!
Дори в Йо, с огромната гравитация на Юпитер, приливите и отливите са малки, защото Йо е достатъчно далеч. В Ако приливите бяха много по-силни, Йо щеше лесно да бъде разкъсан от Юпитер. В Минималното разстояние, за да може един спътник да остане непокътнат, се нарича граница на рош. В След тази точка приливната сила е по-голяма от собствената гравитация на сателита и тя се отделя.
Самият Йо е вулканичен свят поради приливни сили, но това не е изцяло по вина на Юпитер. В Другите Галилееви Луни на Юпитер допринасят за това, че Йо има ексцентрична орбита, което кара орбиталното разстояние на Йо да варира. В Това създава вариации в приливната сила, която усеща от Юпитер, и променящите се приливи и отливи причиняват редовно избутване и изтегляне на кората на Йо, създавайки триене в кората и огромно количество топлина, което се проявява като вулканична активност.
Не става много по-луд от това. Специално благодаря на Джеси Роджърсън за двойна проверка на математиката ми. В Благодаря за четенето! Никога не забравяйте колко невероятна и луда и страшна може да бъде Вселената!
25 мисли на тема „Тежите ли по-малко, когато Луната е над вас? ”
Много интересно! Благодаря
Не позволявайте на Weightwatchers да хванат вятъра на това.
наистина страхотно обяснение и статия. Продължавай с добрата работа
Много благодаря! Чувствайте се свободни да поискате всички теми, които бихте искали да видите!
Мисля, че може би сте използвали грешната дума. Centripedal би трябвало да е центробежен. Ако силата на човека беше центробежна, тя нямаше да „противодейства“ на силата на гравитацията, тя щеше да работи с нея.
Моля, уведомете ме, ако съм прав в това.
Благодаря
Харолд
Благодаря за коментара Харолд. Накара ме да се замисля и прекарах известно време, за да копая по-дълбоко, за да се опитам да подредя всичко. Оказва се (за съжаление), че и двамата грешим.
Първо: Centripetal срещу Centrifugal. Аналогията, която ще използвам, е йо-йо, завъртяно около главата ви. Докато размахвате йо-йо, важното е, че върху него действа нетна сила, тъй като тя се ускорява чрез промяна на посоката. Тази нетна сила е центростремителната сила и е равна на напрежението в въжето. Ако го нямаше, йо-йо вече нямаше да остане в кръгово движение, щеше да отлети по права линия. Тенденцията на даден обект да се противопоставя на кръговото движение понякога се нарича центробежна сила, но не е реална сила. Вместо това инерцията на обекта причинява тази тенденция на права линия. Единствената реална сила, действаща върху йо-йо, е центростремителната сила от напрежението в въжето.
Сега в космоса трябва да правим разлика между контактни и безконтактни сили. Силите за контакт, понякога наричани нормални сили, винаги действат върху нас на Земята. Седнали усещаме стола да се бута нагоре към нас, устоявайки на гравитацията. Всъщност не усещаме гравитацията, усещаме контактната сила на земята, която ни бута, устоявайки на силата на гравитацията.
Ето тук греших. Свързах свободното падане и безтегловността с нулева нетна сила. Космонавтът в орбита се ускорява, те трябва да бъдат, посоката на движението им постоянно се променя, докато се движат по елиптична орбита около Земята. Така че те имат нетна сила, която е центростремителната сила, а също така е гравитационната сила, те са едни и същи в този случай, както при напрежението в йо-йо аналогията. Но няма контактни сили, нищо не ги тласка, което им позволява да усетят силата на гравитацията. Ето какво е свободно падане. Не е липсата на гравитация, а липсата на контактни сили. Това е относителността на Айнщайн в действие.
Още един момент, който да помислите, за да обясните това. Ако бях в асансьор, който падаше към Земята, не виждам нищо извън асансьора, така че се чувствам безтегловност и бих могъл да се нося в асансьора. Гравитацията все още действа върху мен и асансьора, но няма контактни сили от земята или нещо подобно.
Надявам се това да има смисъл и благодаря за коментара! Ще направя промените в публикацията, за да изясня объркването в първоначалното ми обяснение.
Предполагам, че бихте могли да помислите за астронавтите като за „свободно падане“, но мисля, че това е по-скоро състояние на равновесие.
„Свободно падане“ би било по-точно да се опише обект, който се движи с 0 мили в час в сравнение със земната повърхност (допирателна към привличането на гравитацията), следователно той незабавно ще се ускори към земята „свободно“ без центробежни сили борба с гравитацията.
Астронавтите, от друга страна, пътуват с висока скорост, допираща се до земната гравитация. Ако тази скорост се увеличи, те ще „избягат“ от земната гравитация и ще изстрелят в космоса ... ако тази скорост се намали, те ще се спуснат към земната атмосфера, където ще се забавят бързо поради триенето на атмосферата и ще изгорят на земната повърхност.
Резюме: астронавтите не са в свободно падане - може и да падат - но основната сила, която ги поддържа стабилни, е енергията, която ги е ускорила до орбиталната им скорост, съчетана с липсата на каквото и да е, което да ги забави.
Благодаря за вашия пост и сайт и всичко, което правите, за да образовате хората! ! !
Харолд
Благодаря за коментара Харолд - мисля, че този ще бъде решен от моя отговор на другия ви коментар. Радвам се да го обсъдим още малко, ако искате.
Имам въпрос,
Когато сте в космоса, можете да създадете изкуствена гравитация, като обектът, в който се намирате, се завърти. Силата е насочена към натискане към краката ви, докато вървите с глава, обърната към центъра на центрофугата. Но какво ще кажете за луната, която се върти около земята и не се върти. Няма ли гравитацията да е различна от едната страна на Луната от тази, обърната към земята?
Първо Луната всъщност се върти! Но това е, което наричаме „приливно заключено“ към Земята, така че се върти за същото време, необходимо за орбита, 29,5 дни. За да си представите това, представете си, че Земята обикаля около Луната, а не обратното. Ако винаги трябваше да виждаме едно и също лице на Луната, то трябваше да се върти, докато обикаляхме около нея.
„Няма ли гравитацията да е различна от едната страна на Луната от тази, обърната към земята?“
Това е, също поради приливната сила, с изключение на това, че Земята я упражнява върху Луната, но отново тези приливни сили са твърде малки, за да направят разлика за мъничко човече. Що се отнася до центростремителните сили, разликата в ъгловата скорост от близките до далечните страни на Луната е малка и така получената разлика в центростремителните сили е по-малка дори от приливната сила, която обсъдих в статията.
Уведомете ме, ако разбрах правилно вашите въпроси - с удоволствие ще отговоря, ако имате последващи действия.
Благодаря много за това ... Потърсих в Гугъл точно това, тъй като се чудех дали съм по-лек, когато луната беше отгоре.
Обяснението ви беше много задълбочено и след това изпреварихте още един въпрос, когато изчислите отново математиката на Io џ ?
- Диета без отчаяние - Яжте повече, тегнете по-малко
- Тежа ли по-малко на екватора, отколкото при научните въпроси на Северния полюс с изненадващи отговори
- Регистрация на празничното предизвикателство - Яжте интелигентно, движете се повече, тегнете по-малко
- Яжте повече, претегляйте по-малко здравословно тегло, хранене и физическа активност CDC
- Яденето на сини сливи може да помогне за отслабване - The Weigh We Were
