Общото хармонично изкривяване (THD) е измерване, което ви казва каква част от изкривяването на напрежение или ток се дължи на хармониците в сигнала.

Общото хармонично изкривяване (THD) е измерване, което ви казва каква част от изкривяването на напрежение или ток се дължи на хармониците в сигнала. THD е важен аспект в аудио, комуникациите и енергийните системи и обикновено, но не винаги, трябва да бъде възможно най-нисък.

Хармонични честоти на периодично напрежение или ток

Хармониците или хармоничните честоти на периодично напрежение или ток са честотни компоненти в сигнала, които са на цяло число, кратно на честотата на основния сигнал. Това е основният резултат, който показва анализът на Фурие на периодичен сигнал. Хармоничното изкривяване е изкривяването на сигнала поради тези хармоници.

Напрежение или ток, които са чисто синусоидални, нямат хармонично изкривяване, тъй като са сигнал, състоящ се от една честота. Напрежение или ток, които са периодични, но не са чисто синусоидални, ще имат компоненти с по-висока честота, допринасящи за хармоничното изкривяване на сигнала. Като цяло, колкото по-малко периодичният сигнал изглежда като синусоида, толкова по-силни са хармоничните компоненти и толкова по-хармонично изкривяване ще има.

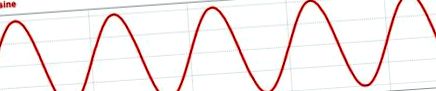
Така че, чисто синусоидален сигнал няма изкривяване, докато квадратна вълна, която е периодична, но изобщо не изглежда синусоидална, ще има много хармонични изкривявания. В реалния свят, разбира се, синусоидалните напрежения и токове не са напълно синусоидални; ще има някакво хармонично изкривяване. Фигури 1 и 2 осигуряват визуални сравнения във времевия и честотния диапазон на синусоидално напрежение и напрежение с квадратна вълна.

измерване

Фигура 1. Синусоидално напрежение и напрежение с квадратна вълна във времевата област.
Фигура 2. Синусоидално напрежение и напрежение с квадратна вълна в честотната област; само квадратната вълна има пикове на хармоничните честоти.

Лесно е да се види хармоничното изкривяване, когато се изследват представянията на времевата област и честотната област на квадратна вълна, но също така е важно да можете да определите количествено хармоничното изкривяване. Следващият раздел показва как да направите това с метриката на общо хармонично изкривяване.

Изчисляване на общото хармонично изкривяване

THD се дефинира като съотношение на еквивалентното средно квадратно (RMS) напрежение на всички хармонични честоти (от 2-ра хармоника нататък) спрямо RMS напрежението на основната честота (основната честота е основната честота на сигнала, т.е. честотата, която бихте идентифицирали, ако изследвате сигнала с осцилоскоп). Уравнение 1 показва математическата дефиниция на THD (имайте предвид, че в това уравнение се използва напрежение, но вместо това може да се използва ток):

  • $$ V _ $$ е средно ефективното напрежение на n-та хармоника
  • $$ V _ $$ е средно ефективното напрежение на основната честота

Тъй като амплитудите на хармониците са необходими за изчисляване на THD, анализът на Фурие може да бъде използван за определяне на THD. За да видим това приложение на анализа на Фурие, нека разгледаме простия пример за квадратна вълна с 50% работен цикъл. Представянето на серията Фурие на квадратна вълна с 50% работен цикъл е следното:

И в разширена форма това е:

Разширената форма е полезна за разглеждане, тъй като подчертава пиковото напрежение (Vpk) на всеки честотен компонент, а THD може да се изчисли чрез определяне на RMS стойността (т.е. $$ \ frac >> $$) на всеки честотен компонент и включвайки ги всички към уравнение 1:

Това уравнение започва да става тромаво, но едно нещо, което трябва да се забележи е, че всеки член в израза има компонент $$ \ frac \ pi> $$. Този компонент може да бъде разложен на множители и тъй като се появява както в числителя, така и в знаменателя, той всъщност се отменя, което оставя израза за THD на квадратна вълна, както следва:

За да се изчисли THD от този израз, е необходима сложна математика. Ако сумирането под квадратния корен в уравнение 5 започва при n = 1, тогава това ще бъде конвергентна поредица, която добавя $$ \ frac $$:

Единствената разлика между израза в уравнение 6 и този в изчислението на THD на уравнение 5 $$ \ left (\ sum _ ^ \ frac \ right) $$ е стойността на $$ \ frac $$, когато n е 1. Тъй като тази стойност е 1, сумирането в израза THD може да бъде пренаписано като:

И накрая, включването на това уравнение обратно в уравнението THD за квадратната вълна (уравнение 5) дава:

Нашето предположение в началото, че квадратната вълна има много хармонични изкривявания, се основава на визуално изследване на квадратната вълна във времето и честотната област. Изчисленията, през които току-що преминахме, потвърждават нашето предположение. Квадратната вълна всъщност има около 48,3% общо хармонично изкривяване, което означава, че RMS на хармониците е около 48,3% от RMS на основната честота.

Измерване на общото хармонично изкривяване

Изчисляването на теоретичната THD може да бъде добро упражнение, но може да е много работа и на практика така или иначе няма да получите идеален сигнал (напр. Перфектна квадратна вълна). Резултатът от тези изчисления следователно може да даде приблизително приблизително THD, което може да получите за даден тип сигнал. На практика THD трябва да бъде измерен, за да се получи RMS стойността на основната честота и всички хармоници. Това измерване може да се направи по няколко начина.

При първия метод филтрите могат да се използват за разделяне на сигнала на две части: сигнал с всички филтрирани хармоници, оставяйки само основната честота, и сигнал с филтрирана основна честота, оставяйки всички хармоници. Тогава RMS стойността на всяка от тези две части може да бъде измерена и THD изчислена:

Предимството на този метод е, че е лесно да се извършат тези измервания. Недостатъкът е, че шумът също ще бъде включен в измерването, така че всъщност получавате измерване на THD плюс шум (въпреки че в аудио системите THD + шумът всъщност също е важно измерване).

Вторият метод за измерване на THD е да се измери амплитудата на основната честота и всяка хармоника и след това да се използват тези измервания за изчисляване на THD с помощта на уравнение 1. Това измерване може лесно да се направи с помощта на спектров анализатор или THD анализатор, който ще изпълни уравнение 1 автоматично . Алтернативна техника за измерване е улавяне на данни за напрежение или ток и след това извършване на Фурие трансформация върху събраните данни. Примерът по-долу очертава как се използва този втори метод.

Пример за измерване на THD

Примерната блок-схема на фигура 3 показва 1 kHz синусоида, преминаваща през усилвател, за да се създаде нова 1kHz синусоида, която има известно кръстосано изкривяване. Тази нова вълна се подава към анализатор на спектъра, който дава графичен дисплей на амплитудата на редица хармоници.

Фигура 3. Система, която въвежда кръстосано изкривяване в сигнал.

Увеличавайки честотния спектър на изкривената изходна синусоида, можем да видим амплитудите на няколко от хармоничните честоти:

Фигура 4. Честотен спектър на синусоидалното напрежение с кръстосано изкривяване.

От този честотен спектър измерих ръчно амплитудата на всяка от хармоничните честоти и записах данните в таблицата по-долу:

Амплитуди на хармоници на изкривена синусоида
Хармонично Амплитуда
1 3.08V
3 0.308V
5 0,159V
7 0,090V
9 0,0487V
11. 0,0253V
13 0,0164V
15 0,010V

Амплитудите на четните хармоници и хармоници над 15-ти са близо 0, така че не ги включих в изчислението си.

Измерените амплитуди се включват в уравнението THD:

(имайте предвид, че мога да използвам амплитудите на напрежението вместо RMS напрежение, защото $$ V_ = \ frac $$ и тъй като $$ \ sqrt $$ се появява при всички условия, той може да бъде разложен и анулиран).

Това изчисление дава THD от 0,118 или 11,8%.

Разбира се, THD анализаторът ще автоматизира процеса на изчисляване на THD от амплитудите на хармониците. Използването на THD анализатор за този сигнал дава стойност от 11,9%, което потвърждава точността на ръчния метод, който току-що преминах.

Значение на THD в системите

Тази статия предоставя известна информация за THD и как да го определим както теоретично, така и в реална (симулирана) система. Но той не е обсъждал видовете системи, при които THD е важно измерване.

THD е важен в няколко типа системи, включително енергийни системи, където нисък THD означава по-висок фактор на мощността, по-ниски пикови токове и по-висока ефективност; аудио системи, където ниското THD означава, че аудио сигналът е по-вярно възпроизвеждане на оригиналния запис; и комуникационни системи, където ниското THD означава по-малко смущения в други устройства и по-висока мощност на предаване на сигнала от интерес.

Потърсете бъдещи статии, където ще вляза в повече подробности за тези специфични видове системи.