Резюме

Ключово съобщение

Връзката между относителната загуба на вода (RWL) и загубата на хидравлична проводимост (PLC) в беловина е силна при иглолистните видове. Ние предлагаме емпиричен модел ( иглолистна крива ) за прогнозиране на PLC от прости измервания на RWL. Подходът се разглежда като нов подходящ инструмент за фенотипиране за чувствителност към суша и предлага надеждна и бърза прогноза за дневни, сезонни или предизвикани от суша промени в PLC.

Контекст

За иглолистните видове сушата е един от основните климатични рискове, свързани със загуба на хидравличен капацитет в беловината, предизвикваща отстъпление или смъртност. По-често срещаните вълни от суша изискват бързи и лесно приложими методи за прогнозиране на чувствителността към суша.

Цели

Насочихме се към разработване на бърз и надежден метод за определяне на процентната загуба на хидравлична проводимост (PLC) и в крайна сметка характеристика на чувствителност към суша P50, т.е. водният потенциал, който причинява 50% загуба на проводимост.

Методи

Измерихме загубата на воден транспортен капацитет, дефинирана като относителна загуба на вода (RWL), заедно с PLC в дървесината на ствола, клоните и фиданките на осем различни иглолистни вида. Използва се инжекция с въздух за индуциране на специфични водни потенциали.

Резултати

Връзката между RWL и PLC беше стабилна за видовете, органите и възрастовите класове. Установеното уравнение позволява бързо предсказване на PLC от прости гравиметрични измервания и по този начин изчисляване на post hoc на P50 (r 2 = 0,94).

Заключение

Подходът се разглежда като подходящ нов инструмент за фенотипиране. Бъдещите потенциални приложения са скрининг на иглолистни дървета за чувствителност към суша и бърза интерпретация на дневни, сезонни или предизвикани от суша промени в съдържанието на вода в ксилема при тяхното въздействие върху загубата на проводимост.

Въведение

Целта на това проучване е да потвърди доста стабилната връзка между PLC и RWL (Rosner et al. 2019) при иглолистни видове, произхождащи от различни екосистеми по целия свят. Подобен подход трябва не само да доведе до бързо прогнозиране на специфични за вида, органите или възрастовите класове хидравлични уязвимости, но също така ще ни позволи да установим количеството вода, останало в ксилема при P50 и P88 (Ψ при 88% PLC). Тествахме зряла и млада дървесина, както и клони на осем различни иглолистни вида с широк спектър от естествени явления от изключително влажна среда (Taxodium distichum) до доста суха среда (Juniperus virginiana). По този начин очаквахме широк диапазон в P50. Повечето от изследваните видове също имат голямо икономическо значение (Abies nordmanniana, Larix decidua, Picea abies, Pinus ponderosa, Pinus taeda, Pseudotsuga menziesii), което допълнително обосновава необходимостта от бързи и надеждни скринингови инструменти за избор на подходящи произход с по-висока толерантност към суша.

материали и методи

Растителен материал

Информация за произхода на растителния материал е предоставена в таблица 1. Бяха изследвани осем различни иглолистни вида, които включваха Abies nordmanniana ((Stev.) Spach), Juniperus virginiana L., Larix decidua Мелница., Picea abies (L.) Карст., Pinus ponderosa П. Лоусън и К. Лоусън, Pinus taeda L., Pseudotsuga menziesii (Мирбел) Франко и Taxodium distichum Л. Рич.

Определяне на загуба на проводимост и относителна загуба на вода

Пробите се сушат при 103 ° С в продължение на 24 часа (Rosner 2017), за да се определи сухо тегло (DW) на везна. Относителната загуба на вода (RWL) при Ψ се изчислява като:

Правилното определяне на SW е от решаващо значение, тъй като свързването на FW с водното съдържание на място в полето би затъмнило връзката между RWL и PLC и не би позволило правилно прогнозиране на PLC (Rosner et al. 2019).

Брой проби, обработка на данни и статистически анализи

Брой извадени дървета, проби и набори от данни могат да бъдат намерени в Таблица 1. Софтуерът SPSS ™ 21.0 е използван за извършване на анализи на данни. Нормалното разпределение беше тествано с теста на Колмогоров-Смирнов. Връзките между чертите бяха приети като значими, ако P стойността беше $$ \ mathrm \ \ ляво (\% \ дясно) = 100/\ ляво (1+ \ exp \ ляво (a \ ast \ ляво (\ Psi -b \ дясно) \ дясно) \ дясно) $$

Параметърът „а”Съответства на наклона на линейната част на регресията и„б”Е P50. P88 се изчислява от тези параметри. Ψ в уравнение (2) се използва тук и след това за водния потенциал. В таблица 2, резултати за „а" и P50 са снабдени със стандартната си грешка и 95% доверителен интервал (CI 95%).

Връзката между точковите измервания и средния PLC и RWL бяха тествани чрез функцията „оценка на кривата“ в SPSS ™ 21.0, където бяха избрани линейни, квадратни или кубични регресии според тяхното прогнозно качество. Избраното уравнение беше използвано за изчисляване на RWL при P50 за всеки вид, орган или възрастов клас. В таблица 3 CI 95% и 95% индивидуални интервали за прогнозиране (PI 95%) за RWL при P50 или RWL при P88 са предоставени. Специфичните за видовете, органите и възрастовите класове средни стойности на PLC (PLCpred) и RWL се определят от уравнение на Weibull (например, Lopez et al. 2005):

Параметърът „° С”Съответства на средния RWL за всички иглолистни дървета, изследвани в изследването, което причинява

Кривите на загубата на вода, т.е. RWL, начертан спрямо Ψ (RWL-Ψ крива), са оборудвани с функцията „оценка на кривата“ в SPSS ™ 21.0. Фитингите с най-високо качество на предсказване (r 2) и беше избрана най-надеждната форма. Функцията „оценка на кривата“ също се използва за установяване на връзката между Ψ и RWL, за да се предскаже Ψ при даден RWL, например RWL при P50 или на P88. В тези криви Ψ е начертан спрямо RWL (крива Ψ-RWL, Таблица 4).

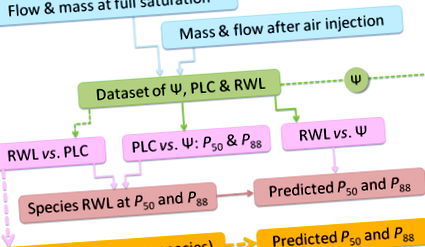
Прогностичното качество на RWL за PLC на ниво вид, орган и възрастова класа беше тествано чрез изчисляване на емпирично моделирано P50 параметъра от RWL при P50 и връзката между Ψ и RWL (крива Ψ-RWL). Същата процедура беше извършена за P88. Прогнозираните стойности на P50 и P88 са снабдени с техните 95% CI и 95% PI (Таблица 4). С помощта на уравнението [3], PLC се прогнозира от измервания на точката на RWL (ако има такива) и средни стойности (Таблица 1). След това, P50 и P88 параметъра (Таблица 5) бяха изчислени с помощта на уравнение [2]. Моделиран P50 и P88 бяха свързани със съответните черти от директно измерени набори от данни. Извършен е линеен регресионен анализ, за ​​да се отговори на изискването за наклон 1: 1. Схема на двата различни подхода е показана на фиг. 1.

прогноза

Диаграма на процедурата за измерване на двата моделни подхода за изчисляване на P50 или P88. Излюпените линии показват процедурата за моделиране на „иглолистната крива“, плътни линии за специфичния за видовете подход за моделиране, за да се предскаже P50 или P88. Наборът от данни включва водния потенциал (Ѱ), RWL (относителна загуба на вода) и PLC (процент загуба на проводимост)

Резултати

Изследваните видове иглолистни дървета варират значително в своята уязвимост към кавитация (фиг. 2, таблица 2). В фиданки, A. nordmanniana имаше най-ниската P50 (- 8,1 MPa) и P. menziesii отглеждани в Австрия са с най-висок P50 (- 5,0 MPa). В клонове, P50 варира от -5,8 MPa в P. menziesii до - 2,4 MPa в T. distichum. Общо взето, P50 е най-високата в дървесината на основния ствол, варираща от -4,9 MPa в P. menziesii до - 2,2 MPa в P. abies. Изследваните видове също варират в техните RWL при дадено прилагане на налягане (Фиг. 2). Например, докато RWL се увеличава само леко с всяко прилагане на налягане през A. nordmanniana фиданки (фиг. 2б), RWL имаше големи увеличения в по-тесни граници на налягането в P. abies дърво на багажника (фиг. 2г).

Точкови измервания на процентна загуба на хидравлична проводимост (PLC) и прогнозни криви на уязвимост, описани в таблица 2 в приложението (a, c, e, g) и на относителна загуба на вода (RWL) и прогнозни криви на загуба на вода, описани в таблица 4 в приложението (b, d, f, h), нанесено спрямо водния потенциал за различни видове иглолистни дървета, органи или възрастови класове

PLC е силно свързан с RWL на ниво, специфично за вида/органа/възрастта (Таблица 3). Средните видове/органи/специфични за възрастта PLC за даден Ψ и PLC, предвидени от съответния набор от данни за RWL (Таблица 3), са следователно силно линейно свързани (Фиг. 3b). RWL при P50 са имали стойности, вариращи от 15% в L. decidua фиданки до 36% в J. virginiana багажник дърво. Чрез видовете/органите/специфичните за възрастта RWL при P50 и връзката между Ψ и RWL (Таблица 4), PМогат да се предвидят 50 стойности, които корелират силно (почти 1: 1) с тези, изчислени от измерения набор от данни (фиг. 4а). Предвижда се P88 беше също така силно свързано с P88, получени от измерени набори от данни (r 2 = 0,98, P Фиг. 3

Връзка между средно измерените PLC и RWL при иглолистни видове, органи и възрастови класове за дадено приложение на налягането (Ψ): „иглолистна крива”(А), предвиден среден PLC, като се използват специфични криви за видове, органи и възраст (Таблица 3 в приложението) (b) и предсказан среден PLC, като се използва„иглолистна крива”(C) свързани както със средните измерени PLC стойности при даден Ψ. Уравнението в графика (а) е както следва: PLCpred = 100 - (100/(exp ((RWL /° С) **д))), където ° С е 30,49 ± 0,52, 95% CI (29,46 31,52) и д е 1,92 ± 0,08, 95% CI (1,75 2,08). Номерът на набора от данни за всичките три парцела е н = 147

Предвидено прилагане на налягане, което е необходимо, за да доведе до 50% загуба на проводимост (P50) от специфични за видове/органи/възраст модели (таблици 2, 3 и 4 в приложението) (а) и P50, изчислено от PLC, предвидено с иглолистна крива (ур. [4]) след корекция на наклон (b), свързана с P50, получени от експериментални набори от данни. Корекцията на наклона (ур. [5]) беше необходима, тъй като нямаше корелация 1: 1 (сиви пунктирани линии) в долната част P50 стойности (фиг. 6 в приложението)

За да се гарантира еднакво тегло на специфичната връзка PLC-RWL, специфична за всеки вид, орган и възрастов клас, бяха използвани средни стойности за даден Ψ за анализ на обединените данни (Фиг. 3а). Връзката между PLC и RWL във всички проби е оборудвана с функцията:

PLCpred е прогнозираната процентна загуба на хидравлична проводимост (фиг. 3в). Повече информация за параметрите на уравнение (4) може да се намери в легендата на фиг. 3. RWL от 30,49% съответства на PLCpred на

63% за всички изследвани екземпляри от иглолистни дървета. RWL от 25,18% след това ще доведе до PLCpred от 50%, а RWL от 45,12% ще доведе до PLCpred от 88% за видове, органи и възрастови класове.

От измерванията на точката на RWL и иглолистна крива, Стойностите на PLCpred бяха изчислени. PLCpred стойности и съответното corresponding, беше използвано за проектиране P50 (Таблица 5). Корелацията между P50 и емпирично моделиран P50 (P50pred) беше здраво (r 2 = 0,94, P $$

_ '> = - 0.75 + 0.82 \ ast

_> \ ляво (^ 2 = 0,97, P

където P50pred ’съответства на P50pred след корекция на наклон. P88pred беше също толкова силно свързан с P88, изчислено от измерени данни (r 2 = 0,98, P 2 = 0,44, P Фиг. 5

Връзка между положителното налягане, което е необходимо, за да доведе до 50% загуба на проводимост (P50) и RWL при P50 (а) и при P88 (б) за различни иглолистни видове, органи и възрастови класове

Дискусия

Това проучване проверява дали може да се установи емпирична връзка между загубата на капацитет за пренос на вода и загубата на водно съдържание при умерените иглолистни видове. Установихме, че е възможно да се предскаже загуба на проводимост и в крайна сметка P50 или P88 за различни видове иглолистни видове, органи и възрастови класове с коефициент на определяне 94% от съвсем прости измервания на RWL и using, използвайки един емпиричен модел (иглолистна крива, Фиг. 3а). Въпреки че RWL кривите и кривите на уязвимост се различават значително между видовете, органите или възрастовите класове (фиг. 2), връзката между RWL и PLC вероятно е доста консервативна (фиг. 3). Обсъждаме защо това може да е така при иглолистните, но не и при покритосеменните растения (Rosner et al. 2019), изследваме връзката между хидравличния капацитет и уязвимостта към кавитация и предлагаме как техниката може да бъде доразвита като бърз и надежден инструмент за фенотипиране.

Защо връзката между RWL и PLC е толкова стабилна?

Връзка между хидравличния капацитет и уязвимостта към кавитация

Фенотипиране: граници на приложение и по-нататъшно развитие на метода

Заключения

Успяхме да изградим едно емпирично уравнение на модела, за да предскажем загуба на проводимост и в крайна сметка P50 за различни иглолистни видове с произход от различни екосистеми. Методът предлага бързо и надеждно прогнозиране на PLC от доста прости и бързи измервания на RWL и and и по този начин може да се приложи като ефективен инструмент за фенотипиране за P50. Бъдещите изследвания трябва да тестват този PLC-RWL при иглолистни видове, които не са включени в това проучване, за да се определи дали връзката е универсална. Познаването на тази връзка може да помогне за интерпретирането на прилични техники, базирани на непряка анатомия, като рентгенова микро-компютърна томография или неутронна радиография. Бъдещите потенциални приложения на новия представен метод са скрининг на дърветата за чувствителност към суша и бърза интерпретация на дневните, сезонните или предизвиканите от суша промени в съдържанието на вода в ксилема при тяхното въздействие върху загубата на проводимост.