Задаване на операции и диаграми на Venn | Линейно програмиране | Вероятност | Statistucs | Поредици и серии
Различни видове проблеми с линейното програмиране
По-долу са изброени няколко важни проблеми с линейното програмиране:
1. Проблеми с производството.
2. Диетични проблеми. При тези проблеми ние определяме количеството на различни видове съставки/хранителни вещества, които трябва да бъдат включени в диетата, така че да сведе до минимум разходите за желаната диета, така че тя да съдържа определено минимално количество от всяка съставка/хранителни вещества.
3. Проблеми с транспортните разходи.
📌 Проблем 1 (Проблем с диетата):
Диетолог желае да смеси два вида храни по такъв начин, че съдържанието на витамини в сместа да съдържа поне 8 единици витамин А и 10 единици витамин С. Храната „I“ съдържа 2 единици/кг витамин А и 1 единица/кг на витамин С. Храната „II“ съдържа 1 единица/кг витамин А и 2 единици/кг витамин С. Закупуването на храна „I“ струва 50 USD на кг и 70 USD за кг храна „II“. Формулирайте този проблем като проблем с линейно програмиране, за да сведете до минимум разходите за такава смес.
✍ Решение:
Нека сместа съдържа x kg храна „I“ и y kg храна „II“. Ясно е, че x≥0, y≥0. Ние правим следната таблица от дадените данни:
| Ресурси | Храна | Изисквания | |
| Аз | II | ||
| (х) | (у) | ||
| Витамин А (единици/кг) | 2 | 1 | 8 |
| Витамин С (единици/кг) | 1 | 2 | 10 |
| Разходи (щ.д./кг) | 50 | 70 | |
Тъй като сместа трябва да съдържа най-малко 8 единици витамин А и 10 единици витамин С, имаме ограниченията:
2x + y≥8
x + 2y≥10
Общите разходи Z за закупуване на х кг храна „I“ и y кг храна „II“ са
Z = 50x + 70y
Следователно математическата формулировка на задачата е: Минимизиране
Z = 50x + 70y… (1)
при спазване на ограниченията:
2x + y≥8… (2)
x + 2y≥10… (3)
x, y≥0… (4).
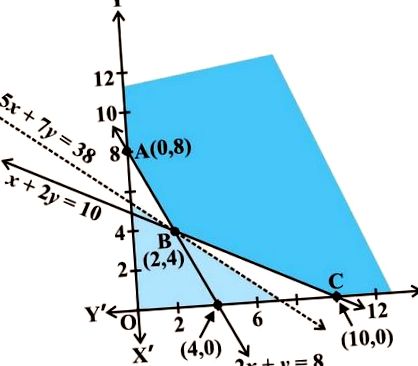
Нека да графираме неравенствата (2) до (4). Възможната област, определена от системата, е показана на фиг. 1. Тук отново наблюдавайте, че възможната област е неограничен.
Нека оценим Z в ъгловите точки A (0,8), B (2,4) и C (10,0).
| Ъглова точка | Z = 50x + 70y |
| (0, 8) (2, 4) (10, 0) | 560 380 ← Минимум 500 |
В таблицата откриваме, че най-малката стойност на Z е 380 в точката (2,4). Можем ли да кажем, че минималната стойност на Z е 380? Не забравяйте, че възможният регион е неограничен. Следователно трябва да начертаем графиката на неравенството
50x + 70г
за да провери дали получената отворена половина равнина има някаква точка, обща с възможния регион. От фиг. 1 виждаме, че той няма общи точки.
По този начин минималната стойност на Z е 380, постигната в точката (2, 4). Следователно, оптималната стратегия за смесване за диетолога би била да смеси 2 кг храна „I“ и 4 кг храна „H“ и при тази стратегия минималната цена на сместа ще бъде USD 380.
Задача 2 показва как може да възникне система от линейни неравенства в приложен проблем.
📌 Проблем 2: Приложение на система от неравенства
Течната част от диетата трябва да осигурява най-малко 300 калории, 36 единици витамин А и 90 единици витамин С дневно. Чаша диетична напитка X осигурява 60 калории, 12 единици витамин А и 10 единици витамин С. Чаша диетична напитка Y осигурява 60 калории, 6 единици витамин А и 30 единици витамин С. Настройте система на линейни неравенства, което описва минималните дневни нужди за калории и витамини.
x = брой чаши диетична напитка X и
y = брой чаши диетична напитка Y.
За да се отговори на минималните дневни изисквания, трябва да бъдат удовлетворени изброените по-долу неравенства.
За калории: 60x + 60y≥300
За витамин А: 12x + 6y≥36
За витамин С: 10x + 30y≥90
x≥0; y≥0
ЗАБЕЛЕЖКА:
Всяка точка в сенчестата област (или на нейната граница) отговаря на минималните дневни изисквания за калории и витамини. Например, 3 чаши диетична напитка X и 2 чаши диетична напитка Y доставят 300 калории, 48 единици витамин А и 90 единици витамин С.
Включени са последните две неравенства, тъй като x и y не могат да бъдат отрицателни.
Графиката на тази система от линейни неравенства е показана вдясно.
📌 Проблем 3: Приложение: Оптимална цена
Задача 2 създаде система от линейни уравнения за проблема по-долу.
Течната част от диетата трябва да осигурява най-малко 300 калории, 36 единици витамин А и 90 единици витамин С дневно. Чаша диетична напитка X осигурява 60 калории, 12 единици витамин А и 10 единици витамин С. Чаша диетична напитка Y осигурява 60 калории, 6 единици витамин А и 30 единици витамин С. Сега, приемете, че диетичната напитка X струва $ 0,12 на чаша, а напитката Y струва $ 0,15 на чаша. Колко чаши от всяка напитка трябва да се консумират всеки ден, за да се минимизират разходите и все пак да се отговори на ежедневните изисквания?
✍ Решение:
Започнете, като оставите x да е броят чаши диетична напитка X и y да е броят чаши диетична напитка Y. Освен това, за да отговорят на минималните дневни изисквания, трябва да бъдат удовлетворени изброените по-долу неравенства.
| За калории: 60x + 60y≥300 За витамин А: 12x + 6y≥36) За витамин С: 10x + 30y≥90 x≥0 y≥0 | > Ограничения |
Графиката на региона, съответстваща на ограниченията, е показана на фигура 2,
За да определите минималните разходи, тествайте C във всеки връх на региона, както е показано по-долу.
В (3, 2); C = 0,12 (3) +0,15 (2) = 0,66 (Минимална стойност на C)
И така, минималните разходи са 0,66 долара на ден и това се случва, когато всеки ден се консумират три чаши напитка X и две чаши напитка Y.
📌 Проблем 4 (Проблем с диетата).
Диетологът трябва да разработи специална диета, като използва две храни P и Q. Всяка опаковка (съдържаща 30 g) храна P съдържа 12 единици калций, 4 единици желязо, 6 единици холестерол и 6 единици витамин А. Всяко пакетче от същото количество храна Q съдържа 3 единици калций, 20 единици желязо, 4 единици холестерол и 3 единици витамин А. Диетата изисква поне 240 единици калций, поне 460 единици желязо и най-много 300 единици холестерол. Колко пакета от всяка храна трябва да се използват, за да се сведе до минимум количеството витамин А в диетата? Какво е минималното количество витамин А?
✍ Решение:
Нека x и y са броят на пакетите храна P и Q съответно. Очевидно x≥0, y≥0. Математическата формулировка на дадения проблем е следната: Минимизиране на Z = 6x + 3y (витамин А)
при спазване на ограниченията
12x + 3y≥240… (÷ 3) (ограничение върху калция)
→ 4x + y≥80… (1)
4x + 20y≥460… (÷ 4) (ограничение за желязо)
→ x + 5y≥115… (2)
6x + 4y≤300… (÷ 2) (ограничение за холестерола)
→ 3x + 2y≤150… (3)
x≥0, y≥0… (4)
Нека да графираме неравенствата (1) до (4).
Възможната област (засенчена), определена от ограниченията (1) до (4), е показана на фиг. 3 и имайте предвид, че тя е ограничена.
[Фиг. 3]
Координатите на ъгловите точки L, M и N са съответно (2, 72), (15, 20) и (40, 15). Нека оценим Z в тези точки:
| Ъглова точка | Z = 6x + 3y |
| (2, 72) (15, 20) (40, 15) | 228 150 ← минимум 285 |
От таблицата откриваме, че Z е минимална в точката (15, 20). Следователно количеството на витамин А при ограниченията, дадени в проблема, ще бъде минимално, ако в специалната диета се използват 15 пакета храна Р и 20 пакета храна Q. Минималното количество витамин А ще бъде 150 единици.
Нека прочетете публикация 👉 Проблеми с транспортните разходи.
- От диетична чивда до мюсли Бъдете здрави с различни видове диетична храна Lifestyle News, The Indian
- Причини за различни видове захарен диабет Библиотека
- Диетичните прегледи на частични храни са различни и ефектът е един
- Диета на извара - видове диети, здравословна диета, храна Всичко е тук
- БЕЗПЛАТНА Е-КНИГА БИБЛИОТЕКА ~ 90 дни Диетичен вестник Хранителен дневник Хранителен вестник ...