Резюме

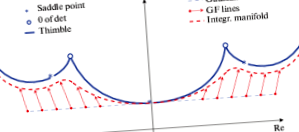
Разглежда се възможността за укротяване на знаковия проблем, който възниква при изследването на фермионни системи с краен химичен потенциал, с използване на алгоритми на невронни мрежи. Решението на проблема със знака е от решаващо значение за текущите изследвания във физиката на кондензираната материя и физиката на кварк-глюонната плазма с висока плътност (ново състояние на веществото, което ще се изследва в ускорителите FAIR и NICA, които са в процес на изграждане). В предложения подход, обучените невронни мрежи грубо възпроизвеждат напръстници на Лефшец: многообразия в сложно пространство, където въображаемата част от действието е постоянна. Демонстрирано е, че обучена мрежа ускорява (в сравнение с общия алгоритъм на градиентния поток) значително изграждането на интеграционния колектор в сложно пространство. Показано е също така, че колебанията на въображаемата част от действието върху приблизителния колектор, дефиниран от невронната мрежа, са все още значително по-малки, отколкото при общия метод за претегляне.

Това е визуализация на абонаментното съдържание, влезте, за да проверите достъпа.

Опции за достъп

Купете единична статия

Незабавен достъп до пълната статия PDF.

Изчисляването на данъка ще бъде финализирано по време на плащане.

използването

ПРЕПРАТКИ

Свръхстудени газове Fermi. Известия на Международното училище по физика „Enrico Fermi“, 164-ти курс, Варена, Италия, 2006 г., Изд. от М. Inguscio, W. Ketterlen и C. Salomon (IOS Press, 2007).

Т. Schäfer и D. Teaney, "Почти перфектна течливост: от студени атомни газове до горещи кваркови глюонни плазми", Rep. Prog. Физ. 72, 126001 (2009); arXiv: 0904.3107 [hep-ph].

L. Rammelmüller, A. C. Loheac, J. E. Drut и J. Braun, „Крайно температурно уравнение на състоянието на поляризирани фермиони при унитарност“, Phys. Преподобни Lett. 121, 173001 (2018); arXiv: 1807.04664 [cond-mat].

M. Troyer и U.-J. Wiese, “Изчислителна сложност и основни ограничения за фермионни квантови симулации на Монте Карло,” Phys. Преподобни Lett. 94, 170201 (2005;, arXiv: 0408370 [cond-mat].

Ф. Карш, Б.-Ж. Schaefer, M. Wagner и J. Wambach, „Към QCD с крайна плътност с разширения на Тейлър“, Phys. Lett. Б. 698, 256–264 (2011); arXiv: 1009.5211 [hep-ph].

А. Базавов, Х.-Т. Ding, P. Hegde, O. Kaczmarek, F. Karsch, E. Laermann, Y. Maezawa, S. Mukherjee, H. Ohno, P. Petreczky, H. Sandmeyer, P. Steinbrecher, C. Schmidt, S. Sharma, W. Soeldner и M. Wagner, “QCD уравнение на състоянието на \ (\ mathcal (\ mathop \ mu \ nolimits_B ^ 6) \) от решетъчна QCD,” Phys. Преп. D 95, 054504 (2017); arXiv: 1701.04325 [hep-lat].

В. Г. Борняков, Д. Л. Бойда, В. А. Гой, А. В. Молочков, А. Накамура, А. А. Николаев и В. И. Захаров, „Нов подход към изчисляването на каноничните разделителни функции в \ (_> = 2 \) решетка QCD при крайна барионна плътност,” Физ. Преп. D 95, 094506 (2017); arXiv: 1611.04229 [hep-lat].

Г. Аарц, „Сложна динамика на Лангевин и други подходи при краен химичен потенциал“, в Сборник от 30-ия международен симпозиум по теория на решетъчното поле, Кернс, Австралия,2012 г., arXiv: 1302.3028 [hep-lat].

G. Aarts, L. Bongiovanni, E. Seiler, D. Sexty и I.‑O. Стаматеску, „Управление на сложна динамика на Лангевин при крайна плътност“, Eur. Физ. J. A 49, 89 (2013); arXiv: 1303.6425 [hep-lat].

D. Шестдесет, „Симулиране на пълен QCD при ненулева плътност, използвайки сложното уравнение на Лангевен,“ Phys. Lett. Б. 729, 108–111 (2014); arXiv: 1307.7748 [hep-lat].

К. Нагата, Дж. Нишимура и С. Шимасаки, „Охлаждане на измервателния уред за проблема със сингулярния дрейф в сложния метод на Лангевен - тест в теория на случайни матрици за QCD с крайна плътност“, J. High Energy Phys. 2016 г. (07), 73 (2016); arXiv: 1604.07717 [hep-lat].

G. Aarts, E. Seiler, D. Sexty и I.-O. Стаматеску, „Сложна динамика на Лангевин и нули на детерминантата на фермиона“, J. Физика с висока енергия. 2017 г. (05), 44 (2017); arXiv: 1701.02322 [hep-lat].

J. Bloch, J. Glesaaen, J. J. M. Verbaarschot и S. Zafeiropoulos, „Сложна симулация на Лангевен на произволен матричен модел при ненулев химичен потенциал“, J. High Energy Phys. 2018 г. (03), 15 (2018); arXiv: 1712.07514 [hep-lat].

K. N. Anagnostopoulos, T. Azuma, Y. Ito, J. Nishimura и S. Kovalkov Papadoudis, „Комплексен анализ на Лангевен на спонтанното нарушаване на симетрията в размерно редуцирани супер модели на Ян-Милс“, J. High Energy Phys. 2018 г. (02), 151 (2018); arXiv: 1712.07562 [hep-lat].

M. Scherzer, E. Seiler, D. Sexty и I.-O. Стаматеску, „Сложен Лангевин и гранични термини“, Физ. Преп. D 99, 014512 (2019); arXiv: 1808.05187 [hep-lat].

Е. Витен, „Нов поглед към интеграла на пътя на квантовата механика,“ arXiv: 1009.6032 [hep-th].

Е. Витен, „Аналитично продължение на теорията на Черн-Саймънс”, в Теория на измервателните уреди на Черн – Саймънс: 20 години след това, Изд. от J. E. Andersen, H. U. Boden, A. Hahn и B. Himpel (American Mathematical Society, 2011), стр. 347–446; arXiv: 1001.2933 [hep-ти].

М. Кристофорети, Ф. Ди Ренцо и Л. Скорцато, „Нов подход към знаковия проблем в квантовите теории на полето: КХД ​​с висока плътност върху напръстник на Лефшец“, Физ. Преп. D 86, 074506 (2012); arXiv: 1205.3996 [hep-lat].

М. Кристофорети, Ф. Ди Ренцо, А. Мукерджи и Л. Скорцато, „Квантови теории на полето на напръстника Лефшец“, в Сборник от 31-ия международен симпозиум по теория на решетъчното поле, Майнц, Германия,2013, arXiv: 1312.1052 [hep-lat].

М. Кристофорети, Ф. Ди Ренцо, А. Мукерджи и Л. Скорцато, „Симулации на Монте Карло върху напръстника на Лефшец: Укротяване на проблема със знака“, Физ. Преп. D 88, 051501 (R) (2013); arXiv: 1303.7204 [hep-lat].

Х. Фуджи, Д. Хонда, М. Като, Ю. Кикукава, С. Комацу и Т. Сано, „Хибрид Монте Карло върху напръстници Лефшец - Изследване на проблема с остатъчните знаци“, J. High Energy Phys. 2013 (10), 147 (2013); arXiv: 1309.4371 [hep-lat].

H. Fujii, S. Kamata и Y. Kikukawa, „Лефшец структура на напръстника в едномерен решетъчен модел Thirring при крайна плътност“, J. High Energy Phys. 2015 г. (11), 078 (2015); arXiv: 1509.08176 [hep-lat].

Y. Tanizaki, Y. Hidaka и T. Hayata, „Lefschetz-thimble analysis of the sign problem in one-site fermion model,“ New J. Phys. 18., 033002 (2016); arXiv: 1509.07146 [hep-ти].

Т. Каназава и Ю. Танидзаки, „Структура на напръстниците на Лефшец в прости фермионни системи“, Дж. Физика с висока енергия. 2015 г. (03), 044 (2015); arXiv: 1412.2802 [hep-lat].

А. Александру, Г. Башар и П. Бедак, „Алгоритъм на Монте Карло за симулиране на фермиони върху напръстници на Лефшец“, Физ. Преп. D 93, 014504 (2016); arXiv: 1510.03258 [hep-lat].

А. Александру, Г. Басар, П. Ф. Бедак, Г. У. Риджуей и Н. С. Уорингтън, „Проблем със знаците и изчисления на Монте Карло отвъд напръстниците на Лефшец“, J. Физика с висока енергия. 2016 г. (05), 053 (2016); arXiv: 1512.08764 [hep-lat].

А. Александру, П. Ф. Бедак, Х. Лам и С. Лорънс, „Дълбоко обучение отвъд напръстниците на Лефшец“, Физ. Преп. D 96, 094505 (2017); arXiv: 1709.01971 [hep-lat].

Ф. Ди Ренцо и Г. Еруци, „Регулиране на напръстниците при работа: от модели на играчки до теории за хирални случайни матрици“, Phys. Преп. D 92, 085030 (2015); arXiv: 1507.03858 [hep-lat].

A. Alexandru, G. Başar, P. F. Bedaque, G. W. Ridgway и N. C. Warrington, „Изчисления на Монте Карло на модела Thirring с крайна плътност“, Phys. Преп. D 95, 014502 (2017); arXiv: 1609.01730 [hep-lat].

A. Alexandru, P. F. Bedaque и N. C. Warrington, „Спин поляризирани нерелативистки фермиони в 1 + 1 измерения“, Phys. Преп. D 98, 054514 (2018); arXiv: 1805.00125 [hep-lat].

А. Александру, Г. Башар, П. Ф. Бедак, Х. Лам и С. Лорънс, „Крайна плътност QED1 + 1 близо до напръстници Лефшец“, Физ. Преп. D 98, 034506 (2018); arXiv: 1807.02027 [hep-lat].

А. Александру, П. Ф. Бедак, Х. Лам, С. Лорънс и Н. С. Уорингтън, „Фермиони при крайна плътност в \ (2 + 1 \) размери със знакови оптимизирани колектори“, Физ. Преподобни Lett. 121, 191602 (2018); arXiv: 1808.09799 [hep-lat].

S. Bluecher, J. M. Pawlowski, M. Scherzer, M. Schlosser, I.-O. Стаматеску, С. Сирковски и Ф. П. Г. Циглер, „Претегляне на напръстници на Лефшец“, SciPost Phys. 5, 044 (2018); arXiv: 1803.08418 [hep-lat].

П. В. Буйвидович и М. И. Поликарпов, „Изследване на Монте Карло на електронотранспортните свойства на еднослойния графен в модела на плътно свързване“, Физ. Преп. Б 86, 245117 (2012); arXiv: 1206.0619 [cond-mat.str-el].

М. В. Улибишев, П. В. Буйвидович, М. И. Кацнелсон и М. И. Поликарпов, „Монте Карло изследване на фазовия преход полуметал-изолатор в монослоен графен с реалистичен потенциал за междуелектронно взаимодействие“, Физ. Преподобни Lett. 111, 056801 (2013); arXiv: 1304.3660 [cond-mat.str-el].

Д. Смит и Л. фон Смекал, „Симулация на Монте Карло на модела на плътно свързване на графен с частично екранирани кулоновски взаимодействия“, Phys. Преп. Б 89, 195429 (2014), arXiv: 1403.3620 [hep-lat].

P. V. Buividovich and M. V. Ulybyshev, “Приложения на решетъчните QCD техники за системи с кондензирана материя,” Int. J. Mod. Физ. A 31, 1643008 (2016); arXiv: 1602.08431 [hep-lat].

М. Hohenadler, F. Parisen Toldin, I. F. Herbut и F. F. Assaad, „Фазова диаграма на модела Kane – Mele – Coulomb“, Phys. Преп. Б 90, 085146 (2014); arXiv: 1407.2708 [cond-mat.str-el].

М. Ulybyshev, C. Winterowd и S. Zafeiropoulos, “Колективни възбуждащи заряди и преходът метал-изолатор в квадратната решетка на модела на Хъбард-Кулон,” Phys. Преп. Б 96, 205115 (2017); arXiv: 1707.04212 [cond-mat.str-el].

М. Кьорнер, Д. Смит, П. Буйвидович, М. Улибишев и Л. фон Смекал, „Хибридно Монте Карло изследване на еднослоен графен с частично екранирани кулоновски взаимодействия при крайна спинова плътност“, Физ. Преп. Б 96, 195408 (2017); arXiv: 1704.03757 [cond-mat.str-el].

C. Wu и S.-C. Джанг, „Достатъчно условие за отсъствие на знаковия проблем във фермионния квантов алгоритъм на Монте Карло“, Физ. Преп. Б 71, 155115 (2015); arXiv: cond-mat/0407272 [cond-mat.str-el].

S. R. White, R. L. Sugar и R. T. Scalettar, „Алгоритъм за симулация на многоелектронни системи при ниски температури“, Phys. Преп. Б 38, 11665–11668 (1988).

S. Beyl, F. Goth и F. F. Assaad, „Преразглеждане на хибридния квантов метод на Монте Карло за модели на Хъбард и електрон-фонон“, Phys. Преп. Б 97, 085144 (2018); arXiv: 1708.03661 [cond-mat.str-el].

I. Goodfellow, Y. Bengio и A. Courville, Дълбоко обучение (MIT Press, 2016).

М. А. Нилсен, Невронни мрежи и задълбочено обучение (Determination Press, 2015).

Г. Цибенко, „Апроксимация чрез суперпозиции на сигмоидална функция“, Математика. Контрол, Сигнали, Сист. 2, 303–314 (1989).

A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga и A. Lerer, „Автоматична диференциация в PyTorch“, в Сборник от 31-ва конференция за невронни системи за обработка на информация, Лонг Бийч, САЩ,2017 г..

Х. Но, С. Хонг и Б. Хан, „Учебна мрежа за деконволюция за семантична сегментация“, в Сборник с доклади от Международната конференция по компютърна визия на IEEE, Сантяго, Чили,2015 г., с. 1520–1528.

J. Long, E. Shelhamer и T. Darrell, „Напълно конволюционни мрежи за семантична сегментация“, в Сборник с доклади от Международната конференция по компютърна визия на IEEE, Сантяго, Чили,2015 г., с. 3431–3440.

Y. LeCun, L. Bottou, Y. Bengio и P. Haner, „Градиентно обучение, прилагано за разпознаване на документи“, в Сборник с доклади от Международната конференция по компютърна визия на IEEE, Сантяго, Чили,2015 г., с. 2278–2324.

А. Крижевски, И. Суцкевер и Г. Е. Хинтън, „Класификация на Imagenet с дълбоки конволюционни невронни мрежи“, в Сборник от 26-та конференция по невронни системи за обработка на информация, езерото Тахо, САЩ,2012 г., с. 1097–1105.

В. Дюмулен и Ф. Визин, „Ръководство за конволюционна аритметика за дълбоко обучение“, arXiv: 1603.07285 [stat.ML] (2016).

O. Ronneberger, P. Fischer и T. Brox, „U-Net: Конволюционни мрежи за биомедицинско сегментиране на изображения“, в Сборник с доклади от Международната конференция по изчисляване на медицински изображения и компютърно-асистирана интервенция, Мюнхен, Германия,2015 г., с. 234–241.

D.-A. Clevert, T. Unterthiner и S. Hochreiter, „Бързо и точно учене на дълбоки мрежи чрез експоненциални линейни единици (ELU);“ arXiv: 1511.07289 [cs.LG] (2015).

K. He, X. Zhang, S. Ren и J. Sun, „Дълбоко остатъчно обучение за разпознаване на изображения“, в Материали от Международната конференция на IEEE по компютърно зрение, Лас Вегас, САЩ,2016 г., с. 770–778.

R. K. Srivastava, K. Greff и J. Schmidhuber, „Магистрални мрежи“, arXiv: 1505.00387 [cs.LG] (2015).

D. P. Kingma и J. Ba, „Адам: Метод за стохастична оптимизация“, arXiv: 1412.6980 [cs.LG] (2014).

O. Ronneberger, P. Fischer и T. Brox, „U-Net: Конволюционни мрежи за биомедицинско сегментиране на изображения“, в Сборник с доклади от Международната конференция по изчисляване на медицински изображения и компютърно-асистирана интервенция, Мюнхен, Германия,2015 г., с. 234–241.