В функцията за производителност по подразбиране на средно квадратична грешка (вж. Обучение и прилагане на многослойни плитки невронни мрежи), всяка квадратна грешка допринася със същото количество към функцията за производителност, както следва:
F = m s e = 1 N ∑ i = 1 N (e i) 2 = 1 N ∑ i = 1 N (t i - a i) 2
Кутията с инструменти обаче ви позволява да претегляте всяка квадратна грешка поотделно, както следва:
F = m s e = 1 N ∑ i = 1 N w i e (e i) 2 = 1 N ∑ i = 1 N w i e (t i - a i) 2
Обектът за претегляне на грешки трябва да има същите размери като целевите данни. По този начин грешките могат да бъдат претеглени според времевата стъпка, номера на пробата, номера на сигнала или номера на елемента. Следва пример за претегляне на грешките в края на времева последователност по-силно от грешките в началото на времева последователност. Обектът за претегляне на грешки се предава като последен аргумент в поканата за обучение .
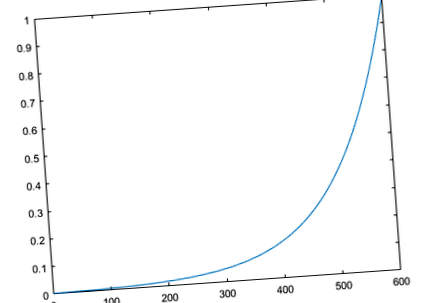
Фигурата илюстрира претеглянето на грешката за този пример. Има 600 стъпки от времето в данните за обучение и грешките се претеглят експоненциално, като последната квадратна грешка има тежест 1, а квадратната грешка в първата времева стъпка има тежест 0,0024.
Отговорът на обучената мрежа е показан на следващата фигура. Ако сравните този отговор с отговора на мрежата, която е била обучена без експоненциално претегляне на квадратните грешки, както е показано в Невронни мрежи със закъснение с времезакъснение при проектиране, можете да видите, че грешките в края на последователността са по-малки от грешките по-рано в последователността. Грешките, възникнали по-късно, са по-малки, тъй като те допринесоха повече за претегления индекс на производителност, отколкото предишните грешки.