Тази статия представя хитър трик за значително съкращаване на размера на параметрите.

Проблем: Когато се занимаваме с данни от Genomics, има твърде малко примери ($ O (10 ^ 3) $) в сравнение с размера на променливата, който обикновено е в порядъка на $ O (10 ^ 6) $. Това е проблем, тъй като при такъв огромен променлив размер той ще съответства на модел с огромни размери на параметрите. Но имаме само малко примери за обучение, което прави модела много по-подходящ за учебния комплект.

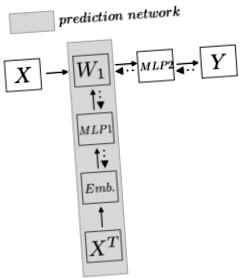
Метод: Първо, нека формализираме проблемите, за да имаме по-ясна картина. Да предположим, че имаме геномни данни с размер $ N $ x $ N_d $ ($ N $ проби и $ N_d $ характеристики/SNP), където $ N \ ll N_d $. Искаме да проектираме модел, за да предскажем дали пробата има определена черта. В този доклад стратификация на населението. Вместо директно да приложи линеен слой в горната част на примера за обучение, който със сигурност включва $ W_1: N_d $ x $ N_h $ размери на параметри, авторът предлага да се използва друга мрежа за прогнозиране на параметрите, по този начин $ W_1 $ не е параметър, но прогноза от мрежата от параметри. Следващата графика, която направих, илюстрира идеята по-ясно:

мрежи

Мрежата на най-горния хоризонт е традиционният модел, при който $ W_1 $ е параметър с огромни размери и води до пренастройване. Авторът използва мрежа за прогнозиране (сивата зона), за да предскаже параметъра. Мрежата за прогнозиране първо транспонира целия набор от данни за обучение и кодира вграждане заедно с функции. След това след подаване на тази функция в многостепенен прецептрон (MLP), мрежата извежда тежестта. Така че на всяка тренировъчна стъпка мрежата за прогнозиране първо ще предскаже $ W_1 $, а след това пример за обучение $ X_n $ ще вземе този $ W_1 $ и ще получи скрито представяне и след това ще направи нормалните стъпки, т.е. MLP и след това softmax, за да предскаже $ Y $. След това в стъпката назад загубата ще се върне на $ W_1 $ и останалата част от мрежата за прогнозиране.

И така, защо мрежата за прогнозиране работи и защо размерът на параметъра ще бъде намален?

Първо, авторът транспонира набора от данни за обучение в $ X ^ T \ в N_d $ x $ N $. По този начин всеки ред съдържа информацията за всички проби за тази функция. Интуитивно той улавя информация за всеки SNP. Така че вграждането може да бъде проектирано така, че да улови най-добре същността на тази функция. Тази статия използва няколко метода за кодиране на вграждания: рандомизиран, SNP2Vec, хистограма за клас и обучен от край до край. Да предположим, че кодираме всяка функция в размер $ N_f $, сега имаме размер $ N_d $ x $ N_f $. Имайте предвид, че това не е параметър, а по-скоро като набор от тренировки.

След стъпката за вграждане приложихме MLP отгоре. Тук идва дедукцията на параметрите. Сега можем да помислим, че имаме набор за обучение с всеки пример с размер $ 1 $ x $ N_f $. Тогава можем да тренираме MLP за размер на параметър $ N_f $ x $ N_h $, за да получим прогноза за размер $ 1 $ x $ N_h $. Имайте предвид, че тук размерът на параметъра е $ N_f $ x $ N_h $. След това чрез изчисляване на всички примери за $ N_d $ чрез това тегло $ N_f $ x $ N_h $ получаваме прогнозата за размер $ N_d $ x $ N_h $, което е размерът на $ W_1 $. По принцип $ (W_1) _j = \ phi (e_j) $, където $ e_j $ представлява вграждане за $ j th $ функция.

След това директно умножаваме истинския пример за обучение на оригинален набор от данни $ X $ с $ W_1 $ и след това прилагаме няколко слоя невронна мрежа и softmax към всяка конкретна задача. Обратното разпространение ще подаде сигнала за грешка до $ MLP1 $, където тежестите в $ MLP1 $ ще станат все по-добри и по-добри за коригиране на прогнозата $ W_1 $.

Сега приключихме. Например, имам работа с данни на GWAS, които имат около $ N_d = 1 * 10 ^ 6 $ и $ N = 6,000 $ данни. Да предположим, че в първия слой искаме скрито представяне с размер $ N_h = 100 $. Така че без тази мрежа размерът на параметъра е $ 1 * 10 ^ 8 $. Сега с мрежата, да предположим, че нашето вграждане е размер $ N_f = 500 $, тогава параметърът в мрежата с параметри е $ N_f $ x $ N_h = 5 * 10 ^ 4 $. Това намалява размера на мрежовия параметър с фактор $ 2000 $.

Тази статия също така отчита голям резултат в степента на погрешна класификация на населението, надминавайки много традиционни подходи.

Интересното от тази статия е, че ако някой размер на параметъра е твърде голям, можем да приложим тази техника, която по същество е въвеждане на междинен агент с по-малко тегло и разглеждаме голямото тегло като проблем за прогнозиране. Ако искаме да възстановим данните във VAE или нещо подобно, можем също да приложим тази техника, за да намалим теглото на крайния слой. Това също добре заобикаля проблема с преоборудването, тъй като сега теглото $ W_1 $ произхожда от богато представяне от вграждания.